
https://tensorflow.google.cn/?hl=zh-cn
“图灵社区”本书页面
http://www.ituring.com.cn/book/2420
开始使用 TensorFlow
借助 TensorFlow,轻松创建可在任何环境中运行的机器学习模型。 通过交互式代码示例,了解如何使用直观的 API。
import tensorflow as tf
mnist = tf.keras.datasets.mnist
(x_train, y_train),(x_test, y_test) = mnist.load_data()
x_train, x_test = x_train / 255.0, x_test / 255.0
model = tf.keras.models.Sequential([
tf.keras.layers.Flatten(input_shape=(28, 28)),
tf.keras.layers.Dense(128, activation='relu'),
tf.keras.layers.Dropout(0.2),
tf.keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
model.fit(x_train, y_train, epochs=5)
model.evaluate(x_test, y_test)深度神经网络(Deep Neural Networks,DNN)
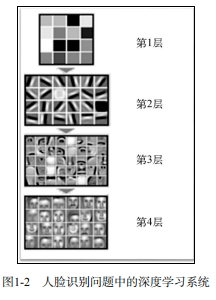
| 在图像分类任务中,这种层级结构叙述如下:一层层的处理块逐渐提取输入图像的特征,每一个块都会继续处理已被前面的块预处理过的数据,提取的特征也越来越抽象。这样,数据就被表示为一种层级结构,这也就是深度学习系统的基础。 |
| 更具体地说,可视化的层级建立过程如下所示。 第1层:系统开始识别明/暗像素 第2层:系统识别边缘和形状 第3层:系统学习到更为复杂的形状和物体 第4层:系统学习人脸由哪些物体定义 |
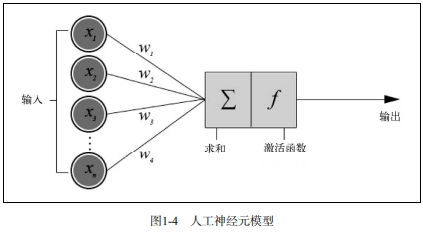
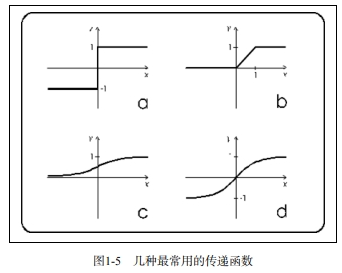
| 神经元的输出,即神经元最终向外界传输的活动信号,是由激活函数对输入信号加权求和计算得出的。激活函数又称传递函数。这类函数的值域一般为1~1或0~1。 以下是几种复杂度和输出彼此不同的激活函数。 阶跃函数:函数会定义一个固定阈值x(如x = 10)。当输入的加权和等于、大于或小于该阈值时,函数将返回0或1。 线性组合:与阶跃函数定义阈值的方式不同,线性组合函数用输入值的加权和去减一个默认值,最终会得到一个二进制值,但一般将其表示为正类(+b)和负类(b)输出。 sigmoid函数:该函数会生成一个S形sigmoid曲线。sigmoid函数一般指一种特殊的logistic函数 |
| 发明了更为复杂的激活函数, 可以使神经元实现更多功能,下面列举其中几种: 双曲正切函数 径向基函数 圆锥曲线函数 softmax函数 |
| 神经网络激活函数中的权重是要靠训练得出的。 虽然在神经网络架构的实现过程中,激活函数的选择非常重要,但研究表明,在保证训练过程正确的前提下,不同激活函数产生的输出质量差距并不太大。 |
| a:阶跃函数 b:线性函数 c:值域为0~1的sigmoid函数 d:值域为1~1的sigmoid函数 |
| 1.4 人工神经网络的学习方式 |
| 1.4 人工神经网络的学习方式 | |
| 1.4.1 反向传播算法 * 一种监督学习算法。 | |
| 该算法训练过程: (1) 以随机权重初始化网络 (2) 对于每个训练样本,重复以下过程 | 前向传播:计算网络产生的总误差,即网络输出与正确输出的差值。 反向传播:从输出层到输入层,反向遍历所有层。 |
| (3) 在反向遍历过程中,根据上一层的误差和对应权值,逐层计算网络内部各层误差,从而将总误差从输出层向隐藏层反向传播,直至传播到输入层。 | |
| (4) 根据各层误差调整各层权重,以最小化误差函数。此为反向传播算法的权重优化步骤。 当验证集上的误差开始增加时,训练终止,因为此时网络可能已经开始过拟合。换言之,网络为了更好地拟合训练数据而牺牲泛化能力 |
1.4.2 权重优化
采用一种数值迭代算法——梯度下降法(Gradient Descent,GD)