【Stardust · 理论物理初阶】 篇二十
“从人类历史的长远观点来看——例如过一万年之后再回头来看——毫无疑问,在19世纪中发生的最有意义事件将被认定为是麦克斯韦对电磁学规律的发现。与这一重大科学事件相比,同一个十年中发生的美国内战(南北战争)将降为一个地区性琐事而黯然失色。”
—— 费曼
【一】麦克斯韦方程组
◆ 位移电流的引入
◆ 麦克斯韦方程组
◆ 含有磁荷的麦克斯韦方程组
【二】电磁波与信息时代
◆ 电磁波的预言
◆ 电磁波的传播速度 · 波动光学
◆ 电磁波的发现
◆ 信息时代:浪潮之巅
【三】电磁场与守恒律
◆ 电磁场的物质性
◆ 电磁场的能量与能量守恒
◆ 电磁场的动量与动量守恒
◆ 电磁场的角动量与角动量守恒
◆ 电磁单位制
上回说到:法拉第怀揣着“磁生电”的信念持之以恒的探索,终于发现了电磁感应现象,并揭示了变化的磁场激发电流的规律——后来被进一步概括为变化的磁场能够激发电场。这一发现不但再一次打通了“电”与“磁”之间的鸿沟,更是开创了电气时代的新纪元。从此,人类能支配的能量、能创造的财富和能活动的空间都被大幅扩展,世界的面貌和生活的方式也被深刻改变。
迄今为止,我们已知的所有电磁学定律——无论是库仑定律、高斯定理、毕奥-萨伐尔定律还是法拉第定律,皆属于“实验定律”的范畴,也即是从实验中总结得到的规律,还没有进行系统的理论总结。而法拉第的伟大发现以及他所提出的精妙“力线”概念,使得进行这种理论总结的时机已然成熟。在过去,像诺依曼或韦伯这样的科学家也尝试过对库仑以来的所有电磁学规律进行理论总结,但他们相信自牛顿以来便占据统治地位的“超距作用”理论——即认为电磁力的传播就像引力的传播一样,是不用花时间的,即便是两个相距遥远、没有任何接触的物体,它们之间的电磁力也是“一瞬间”就能被感应到——这使得他们建立统一理论的愿望没有取得成功。而法拉第的“力线”则指出弥漫在空间中的“力线”才是传播电磁力的“介质”——这便是“场”的原形,法拉第将所有电磁力看作是电荷(电流)与它所在位置的场的近距作用。事实证明法拉第的猜想是可靠的,而建立电磁场统一理论的光辉使命最终的完成者便是一位法拉第思想的追随者——卓越的英国物理学家麦克斯韦。
法拉第和麦克斯韦两个人截然不同。法拉第是一位优秀的实验家,同时早年并没有受过太多数学教育,所以他更多依靠的是自己深刻的物理直觉和强大的洞察力,所以他的工作侧重于定性的表达,在定量的数学表述方面则是欠缺的。麦克斯韦则比法拉第小40岁,出生在爱丁堡的科学世家,从小对数学更为着迷,年轻时就被法拉第的思想吸引住了,下定决心要将法拉第的物理思想用数学公式定量化地表达出来。于是,1855年,年仅24岁的麦克斯韦发表了他的第一篇论文《论法拉第的力线》。法拉第在1857年的回信中表达了他对麦克斯韦工作的称赞:
我亲爱的先生,我接到你的论文,为此深为感谢。我并不是说我要感谢你是因为你谈论了“力线”,因为我知道你已经在哲学真理的意义上处理了它;但你必然以为这项工作使我感到愉快,并给予我很大的鼓励去进一步思考。起初当我看到你用这样的数学威力来针对这样的主题,我几乎吓坏了。后来我才惊讶地看到这个主题居然处理得如此之好!
——在法拉第的鼓励下,麦克斯韦继续向电磁学的更深处前行,尝试建立电磁场的统一理论。这不仅仅是对过去的成就进行总结与数学表述,更重要的是发掘这背后深刻的物理本质。例如:运动变化的电场与磁场与静电场、静磁场的区别在哪?为什么变化的磁场能够产生电场?法拉第正是沿着“‘电生磁’的反过程是‘磁生电’”的思路发现电磁感应的,那么“变化的磁场产生电场”的反过程又是什么?变化的电场能够产生磁场吗?
终于,麦克斯韦以自己的艰苦努力集齐了所有的宝石和珍珠,构筑了经典电磁场的统一理论,物理学中最优美最伟大的方程组之一即将横空出世。而这个方程组中隐藏的“彩蛋”,不但通向物理学最高远的天空,更是继法拉第之后又一次掀起了科技革命的浪潮,将人类社会再次提升到一个全新的高度。
上帝写下了这个方程组,于是,世界上有了光。
【一】麦克斯韦方程组
◆ 位移电流的引入

让我们回顾我们已知的电磁学规律,正如之前所说它们都属于实验定律的范畴。不难写出它的微分形式:
(高斯定理)(法拉第定律)(高斯磁定理)(安培定理){∇⋅E=ρϵ0(高斯定理)∇×E=−∂B∂t(法拉第定律)∇⋅B=0(高斯磁定理)∇×B=μ0J(安培定理)

以及积分形式:
(高斯定理)(法拉第定律)(高斯磁定理)(安培定理){∮SE⋅dS=1ϵ0∫VρdV(高斯定理)∮CE⋅dl=−∫S∂B∂t⋅dS(法拉第定律)∮SB⋅dS=0(高斯磁定理)∮CB⋅dl=μ0∫SJ⋅dS(安培定理)
——也就是说,之前我们所发现的所有关于电磁场的规律,归根到底都是在关注电场E和磁场B这两个矢量场的散度和旋度!这样便可以列出四个方程。而对于一个矢量场而言,散度和旋度得到确定便意味着场本身得到确定。
这些方程组看起来很漂亮,似乎已经正确地揭示了电磁场的一切规律。但是麦克斯韦在考察过往的理论成果时敏锐地意识到:这些方程组仅从理论层面上看就存在着一处致命的矛盾。
矛盾出在哪呢?我们已经知道“旋度的散度总为零”,换言之假设我们对第二个与第四个方程(分别是电场和磁场的旋度方程)再求散度,就应该得到零。对法拉第定律(电场旋度)试一试,得到的是:
∇⋅(∇×E)=∇⋅(−∂B∂t)=−∂(∇⋅B)∂t=0
没有问题。但对安培定理(磁场旋度)试一试,得到的将是:
∇⋅(∇×B)=∇⋅(μ0J)=μ0∇⋅J
——按道理来说右边也必须恒为零。但是我们又已经知道:电流的散度为零( ∇⋅J=0)只对稳恒电流适用,一旦超出了静磁学的范畴(出现了变化的电场),则这一点是必然不成立的。
我们举一个例子——假设我们在给一个电容器充电。对于同样一个回路C,我们取以它为边界的曲面S1使导线从中穿过,这时我们显然可以测到有电流J从中通过,由此可以计算出回路C上激发出的磁场。但是当我们选择同样以C为边界的另一个(“气球形的”)曲面S2使之从电容器两极板间通过,由于电容器两极板之间并没有导线(甚至可能是真空的),自然也没有电流的传导,于是J=0,根据安培环路定律会得到B=0,即回路C上并没有磁场!对于同样一条回路上的磁场计算出了两个截然不同的结论,这就说明安培定理一定出现了什么问题。
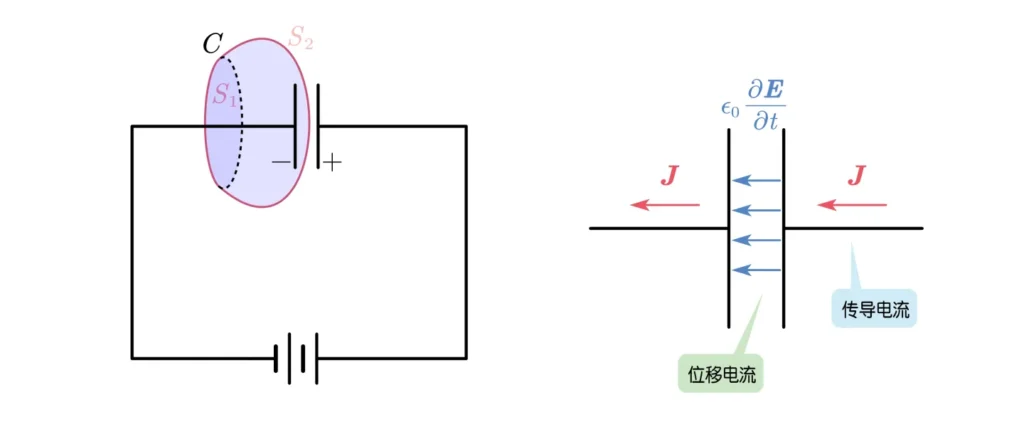
电容器两极板间发生了什么呢?这里虽然没有传导的电流,但是因为两极板上电荷在不断聚集,极板间的电场也在不断增强,因此这里有变化的电场!麦克斯韦尝试将表征电场随时间变化的一项增加到安培定理中,即:
∮CB⋅dl=μ0∫SJ⋅dS+μ0∫Sϵ0∂E∂t⋅dS
微分形式写为:
∇×B=μ0J+μ0ϵ0∂E∂t
——增加了这一项便能够消除以上的困惑!让我们再次验证此时磁场旋度的散度,为:
∇⋅(∇×B)=∇⋅(μ0J+μ0ϵ0∂E∂t)=μ0(∇⋅J+∂ρ∂t)=0
——非常完美,这是因为电流的连续性方程(电荷守恒)∂ρ∂t+∇⋅J=0自然成立。
麦克斯韦新增加的这一项被称作“位移电流”项,位移电流的定义为Jd=ϵ0∂E∂t,即反映电场随时间的变化。他将位移电流与一般的由电荷运动所引起的电流J(也叫传导电流)等同视之,它们共同组成了安培定理里面的电流项!当然,你或许会好奇为什么它被麦克斯韦称作“位移电流”,事实是因为麦克斯韦当初添加这一项是基于历史上的某些其他动机(而不是出于想让旋度方程成立,现在有连续性方程来救场只能算是个“意外惊喜”),如今我们意识到“位移电流”这样的说法并不太恰当,但是由于这个名字从麦克斯韦开始一直沿用至今,我们也就一直用了下去。
但无论如何,麦克斯韦所添加的这一项给我们的最重要的启示是:变化的电场也能产生磁场!换言之,法拉第定律的相反过程被发现了!“变化的磁场产生电场,变化的电场产生磁场”——在静电、静磁问题中看似彼此独立、不存在任何耦合的电场与磁场,在运动变化的过程中却是紧密联系,相伴存在而又互相创生!电场和磁场的内在统一性再一次得到鲜明的彰显。
在通常的实验中,位移电流Jd=ϵ0∂E∂t比起传导电流J一般较小,故而法拉第等人在实验中难以观察到。也就是说,麦克斯韦对安培定理方程的推广并非基于实验,而是纯粹理论的思考与洞察,是创造性思维的结晶。“位移电流”的概念同上一篇中提到的(其实也是麦克斯韦提出的)“涡旋电场”的概念一样,是麦克斯韦在建立电磁场理论过程中的重大突破,是从法拉第的实验到最终的电磁场理论间的一座渡桥。
◆ 麦克斯韦方程组
至此,我们所需要的四个方程已经全部完备——它们分别表征了电场和磁场的散度与旋度。1864年,麦克斯韦向英国皇家学会宣读论文《电磁场的动力理论》,1873年更是出版了《电磁学理论》一书。他系统总结并升华了从库仑到法拉第电磁场研究的全部成就,他所归纳出的整个电磁场理论便是我们所说的——光辉的麦克斯韦方程组。
麦克斯韦方程组的微分形式写作:
{∇⋅E=ρϵ0∇×E=−∂B∂t∇⋅B=0∇×B=μ0J+μ0ϵ0∂E∂t
麦克斯韦方程组的积分形式写作:
{∮SE⋅dS=1ϵ0∫VρdV∮CE⋅dl=−∫S∂B∂t⋅dS∮SB⋅dS=0∮CB⋅dl=μ0∫S(J+ϵ0∂E∂t)⋅dS
——短短四行公式就描述了真空中电磁场所有的运动和行为!麦克斯韦方程组揭示了电磁场理论的整个内部作用和运动行为。通过观察这四个方程,我们可以得出以下结论:电荷和电流可以激发电磁场,而且变化的电场与变化的磁场也可以互相激发。电荷激发的电场是无旋场、变化的磁场激发的电场是有旋场,而无论是电流激发的磁场还是变化的电场激发的磁场都是有旋场。实际上,如果我们更加强调作为“源”的ρ和J,则麦克斯韦方程组还能写成如下更加清晰的形式:
{∇⋅E=ρϵ0∇×E+∂B∂t=0∇⋅B=0∇×B−μ0ϵ0∂E∂t=μ0J
——这种形式将所有的场(电场E和磁场B)都放在了左边,将所有的源(电荷ρ与电流J)都放在了右边,强调所有的电场与磁场归根结底都是由电荷和电流生成的。只要已知了ρ和J的分布,就一定能计算出空间中E和B的分布——然而一旦生成,电磁场便可以独立于电荷而存在,这更深一步揭示了电磁场的物质属性。从此,麦克斯韦电磁场理论被彻底建立起来——麦克斯韦方程组反映的是电荷与电流如何激发场的,再加上描述场如何给电荷与电流力的作用的洛伦兹力公式f¯=ρE+J×B,便已经完全描述了电磁场的运动规律和电磁场与带电物质的相互作用,几乎概括了经典电磁学(或经典电动力学)中已知的所有理论。原则上一切宏观的电磁场问题皆可以用它解决。
麦克斯韦方程组紧凑而优美,是用数学语言描述自然的成果,开创了场理论的先河。后人曾借歌德在《浮士德》中的话评论麦克斯韦方程组:“这种符号难道不是出自上帝之手吗?”事实上,数学从本质上讲便是一种语言,即自然的语言或者说上帝的语言。而物理嘛,便是上帝用数学语言写下的诗歌。
◆ 含有磁荷的麦克斯韦方程组
劳厄曾在《物理学史》中评价:“麦克斯韦方程组,具有美学上真正完美的对称形式。”然而,如果我们采用更“挑剔”的眼光去观察麦克斯韦方程组,我们就会发现电荷密度ρ和电流密度J这两种“源”的存在对电场与磁场的对称性有所破坏。事实上,如果我们相信世界上还存在着“磁荷”,并将对应的“磁荷密度”记作ρm、“磁流密度”记作Jm(相应地,电荷密度记作ρe、电流密度记作Je),则“超越完整版”的麦克斯韦方程组应该写成:
{∇⋅E=ρeϵ0∇×E=−μ0Jm−∂B∂t∇⋅B=μ0ρm∇×B=μ0Je+μ0ϵ0∂E∂t
——换句话说,如果承认磁荷存在,则方程组中将会补上缺失的两项,电场和磁场也便成为完全对称的、地位对等的存在。(不要被那些讨厌的ϵ0与μ0所迷惑,它们仅仅是因为单位制的原因出现的系数。你如果把所有的E换成B,把所有的B换成−μ0ϵ0E,你会发现还能得到原来的结果。)所以从某种意义上来看,麦克斯韦方程组还是很欢迎磁荷的存在,因为它能够被完美融合进来而得到更对称的方程。但很不幸的是,自然界中并没有发现磁荷,因此在我们的宇宙中——电场和磁场依然不是完全对等的。
【二】电磁波与信息时代
◆ 电磁波的预言
麦克斯韦方程组指出“变化的电场产生磁场,变化的磁场产生电场”,也就是说电场和磁场可以“一环扣一环”地交替变化,这意味着电磁作用在空间里很有可能是以某种波动形式传递的。循着这样的思路,麦克斯韦为我们暗示了一个“精灵”——电磁波的存在。
对于一个没有“源项”,即不存在电荷与电流的空间中(真空中,ρ=0、J=0),此时麦克斯韦方程组可以简化为:
{∇⋅E=0∇×E=−∂B∂t∇⋅B=0∇×B=μ0ϵ0∂E∂t
第一种思路是研究电场E。从法拉第定律的式子出发,两边求旋度,会得到∇×(∇×E)=−∂∂t(∇×B)再利用上面讲过的矢量公式∇×(∇×E)=∇(∇⋅E)−∇2E,代入其他公式后得到:
∇2E−μ0ϵ0∂2E∂t2=0
——请再次告诉我它的名字!
还是一个波动方程!
没错,第十三篇中描述一切波动的普遍方程∂2u∂t2=v2∇2u同样可以完全对应此时电场所满足的规律。由此我们可以认为电场E在空间中就是以简谐波的形式传播!因此,电场E(x,t)必然满足简谐波的通用形式:
E(x,t)=E0ei(k⋅x−ωt)
第二种思路是研究磁场B。方法完全类似,这次改从安培定律的式子出发并两边求旋度,得到的是∇×(∇×B)=−μ0ϵ0∂∂t(∇×E),同样利用矢量代数公式∇×(∇×B)=∇(∇⋅B)−∇2B,再用其他公式代入,将得到几乎完全一模一样的一个波动方程:
∇2B−μ0ϵ0∂2B∂t2=0
——因此磁场同样以简谐波的形式传播,满足:
B(x,t)=B0ei(k⋅x−ωt)
——所以,一旦空间中任何一处存在一个周期变化的电场(或磁场),它将在它周围的空间激发出一个变化的磁场(或电场),而这个变化的磁场(或电场)又能在更远一点的空间激发出一个变化的电场(或磁场)……最初的振荡必将以波动的形式向外越传越远!作为场源的电场或磁场,其振荡称作电磁振荡,而这种传播出去的波就是麦克斯韦所预言的电磁波。
◆ 电磁波的传播速度 · 波动光学
麦克斯韦不但预言了真空中可以传播电磁波,还利用波动方程很轻松地计算出了电磁波传播的速度。比照波动方程,我们很容易可以计算出电磁波的波速v只和ϵ0与μ0两个常量有关,也就是:
v=1μ0ϵ0
这个结论看似平平无奇。但只要我们代入具体数值(ϵ0=8.85419×10−12F/m、μ0=4π×10−7H/m),我们其实是可以将波速v真正算出来的。可以算出,它便是:
v=2.99792×108m/s
——这个数字看上去很眼熟:居然和光速相等!
没错,它就是光速c。
这无疑是一个令人惊奇的结论。为了进一步将它说明清楚,我们要再次回到“光”的故事之中。
早在第五篇中,我们就提到,尽管对于光的传播现象的研究从很早就已开始,但对于“光是什么”的争论已经绵延起伏了三个世纪——主要分为针锋相对的两派,一派认为光是粒子,一派认为光是波动。
“粒子派”的开创者是牛顿,他认为光是由许多高速运动的微小粒子所组成的,而这些粒子的运动自然符合牛顿定律。从“粒子派”的观点出发,可以很轻松地解释光的直线传播以及影子的形成,还可以通过弹性碰撞来说明反射定律。再根据引力的观点,假设密度越大的物质对光微粒的“引力”越大,则一旦光从一种物质进入另一种物质时就会被吸引而折向密度较大的物质那边,这也解释了折射定律。——一切看上去都很完美。由于牛顿的崇高地位和影响力,在整个十八世纪,“粒子派”长期占据统治地位,大多数的人对“光是一种微粒”深信不疑。
然而,“粒子派”还遇到了不少棘手的问题——首先说不通的一件事情就是:两束交叉的光是怎么做到能交叉通过而彼此不发生任何干扰的?如果执着于光是微粒,则必须要强行认为这些微粒彼此之间不会发生任何碰撞,这显然是不太可能的,而另一大门派——“波动派”却能对这一现象做出很好的解释。“波动派”的开创者是惠更斯,他认为光是类似水波的波动,光的传播并不意味着物质的输送,只是振动状态的传递。我们已经知道,两支波可以相互叠加、穿越而过而互不干扰。除此以外,“波动派”同样也能解释光的反射、折射、双折射等现象。但“波动说”同样存在一些难题——如果说光是像声波那样的波动,那么它遇到障碍物时便应当绕射而过(就好像呆在房子里的人也能听到外面的声音一样),与光直线传播、无法透过障碍物的现象不符。另外,波的传播总需要某些介质吧,光如果是一种波,它传播的介质又是什么呢?
“波动派”长期被“粒子派”压制,直到19世纪初——1801年,英国医生兼物理学家托马斯·杨通过著名的双缝干涉实验,发生了光的干涉现象;1818年法国工程师菲涅尔演示了光的小孔衍射现象,1821年德国物理学家夫琅禾费发明了基于衍射现象的光栅——人们终于意识到,之前没有发觉光的衍射(绕射)现象仅仅是因为光的波长相比于日常生活的尺度太小罢了!干涉与衍射都是只属于波的性质,这些发现使得“波动派”真正圆满地解释了当时已知的所有光现象,在与“粒子派”的争执中占据上风。1817年,托马斯·杨基于对光偏振现象的系统研究,进一步提出了:光是一种横波。
而对于“粒子派”和“波动派”的最终裁决还要依赖于介质中光速的测定。很早人们就开始好奇:光传播是无限快呢,还是存在一个有限的速度?伽利略曾尝试了许多测量光速的实验方法,但都由于光速过大而无功而返。最早成功的光速测定是在天文观测中进行的,后来菲索和傅科发展出了在实验室里测量光速的方法,后续还有许多科学家对光速的测量方法进行改良,让光速的测量越来越精确。傅科所测量的光在空气中传播的速度约为v=2.98×108m/s(与今天的结论已经非常相近了),而光在水中传播的速度却要更慢,只相当于空气中传播速度的大约3/4。
——这个结论进一步给予了“粒子派”沉重的打击。按照牛顿“粒子派”的观点,水的密度比空气高,倘若光是微粒,则水对光微粒的“引力”应当更强,光在水中传播应当比在空气中传播更快才是!除此之外,当时还发现了更多与光的波动性有关的实验现象,而且“波动派”的理论对此都做出了合理的解释。从此,“光是一种波”的观念彻底被人们接受,开创了光的波动理论——波动光学——的全盛时期。由此,“波动派”大获全胜,“粒子派”进入蛰伏。但此时我们依然还有最后一个疑问:那么光究竟是什么样的波呢?
起初人们认为光波也是类似于声波的机械波,但这样的想法不但与光是横波等等事实矛盾,也再一次将我们代入了那个关于“介质”的困局。“波动派”最开始设想:光赖以传播的介质是“以太”。“以太”(Aether)的词源是古希腊亚里士多德设想的“第五元素”,“波动派”们设想这是一种连续的弹性介质,它充满整个“空虚”的空间,并渗透在一切物体之中。可如果相信“以太”的存在,那么这种弹性模量可能比钢还大的物质充斥了整个宇宙空间,我们却感受不到它的丝毫阻力,这是根本无法解释的难题。更有可能的是“以太”并不存在,而这无疑又让看上去已经十分稳固的“波动说”再次出现了裂痕,我们必须对“光”这种波动寻找机械波以外的其他解释。
——而如今,麦克斯韦预言了电磁波的存在,还得出了一个惊人的结论:电磁波的传播速度应当和光的传播速度相等。
这是否意味着:光波更有可能和电磁波有关?
又或者…… 光,本来就是一种电磁波?
◆ 电磁波的发现
正如前文所说,麦克斯韦的方程组统一了电磁场理论,预言了电磁波的存在,还计算出电磁波以光速传播。他曾明确写下:“……我想两个测定结果如此一致,这充分说明光和电磁是同一物质的两种形态,可以说光是一种遵循电磁定律在场中传播的电磁扰动。”然而麦克斯韦毕竟只有理论推导,而无实验依据,最初并没有得到人们的广泛接受。德国的物理学家赫兹是麦克斯韦的坚定支持者,他致力于为麦克斯韦的理论寻找实验方面的证明。
直到1887年,赫兹才以高超的实验技术在历史上直接验证了电磁波的存在。它在感应线圈两端两极上各接一根铜棒,铜棒末端焊有一对磨光的黄铜球,这对黄铜球靠得很近。当感应线圈猝然间产生一个脉冲时,这对黄铜球上会积累大量的异号电荷,产生强大的电势差以击穿中间的空气,也就是发生了火花放电,长期循环构成一种电磁振荡。而赫兹发现:这种效应可以被距离很远的天线接收!这说明火花放电引发的振荡现象能够辐射到很远的地方,而且天线上接收到的频率和火花放电(波源)处电磁振荡的频率相同,这便意味着这种振动就是以电磁波的形式传播出去的。紧接着,赫兹又做了一系列的实验,证明了电磁波具备波的性质,同时还具备反射、折射、干涉、衍射、偏振等和光有关的一切性质,且电磁波的传播速度确实与光速相等——“光是一种电磁波”就此成为不争的事实。这样一来,“以太”介质也就不再需要,因为电磁波的传播不需要任何介质,在真空中就能传播,它靠的是电场和磁场的相互“激发”,而电场和磁场本身就是一种形式的物质。
赫兹的实验给了麦克斯韦的电磁场理论决定性的证明。从此麦克斯韦一统“光”、“电”、“磁”三大门派——电磁学和光学再也不是彼此独立的领域,而是看起来虽不相干却有着共同本质的统一体。可惜的是,这一年,麦克斯韦已经离开人世八年了。
直到今天,我们对电磁波的认识是:电磁波的传播意味着空间中的各点都存在电场E和磁场B,而电磁波实际传播的就是电场E和磁场B的振动,它们都按正弦规律变化,且始终保持频率和相位相同。如果将E(x,t)=E0ei(k⋅x−ωt)和B(x,t)=B0ei(k⋅x−ωt)代入麦克斯韦方程组,我们将得到:(其实就是将每一个∇改写为ik,将每一个∂∂t改写为−iω)
{ik⋅E0=0ik×E0=iωB0ik⋅B0=0ik×B0=iωc2E0
——第一行和第三行意味着电磁波的传播方向(即波矢k的方向)与电场E与磁场B的方向都垂直,即k⊥E、k⊥B,所以电磁波是横波。第二行与第四行联立得到(ω2c2−k2)E0=0,而该方程有非零解的条件便是ω2c2−k2=0,即ωk=c,代入第二行可以得知复振幅之间的关系E0=cB0,这意味着任意一点处电场和磁场的大小是成比例的,电场的大小是磁场大小的c倍,同时电场E与磁场B互相也是垂直的(E⊥B),电磁场传播的方向和E×B的方向相同(也就是说E、B和k的方向形成了一个右手螺旋的关系)。
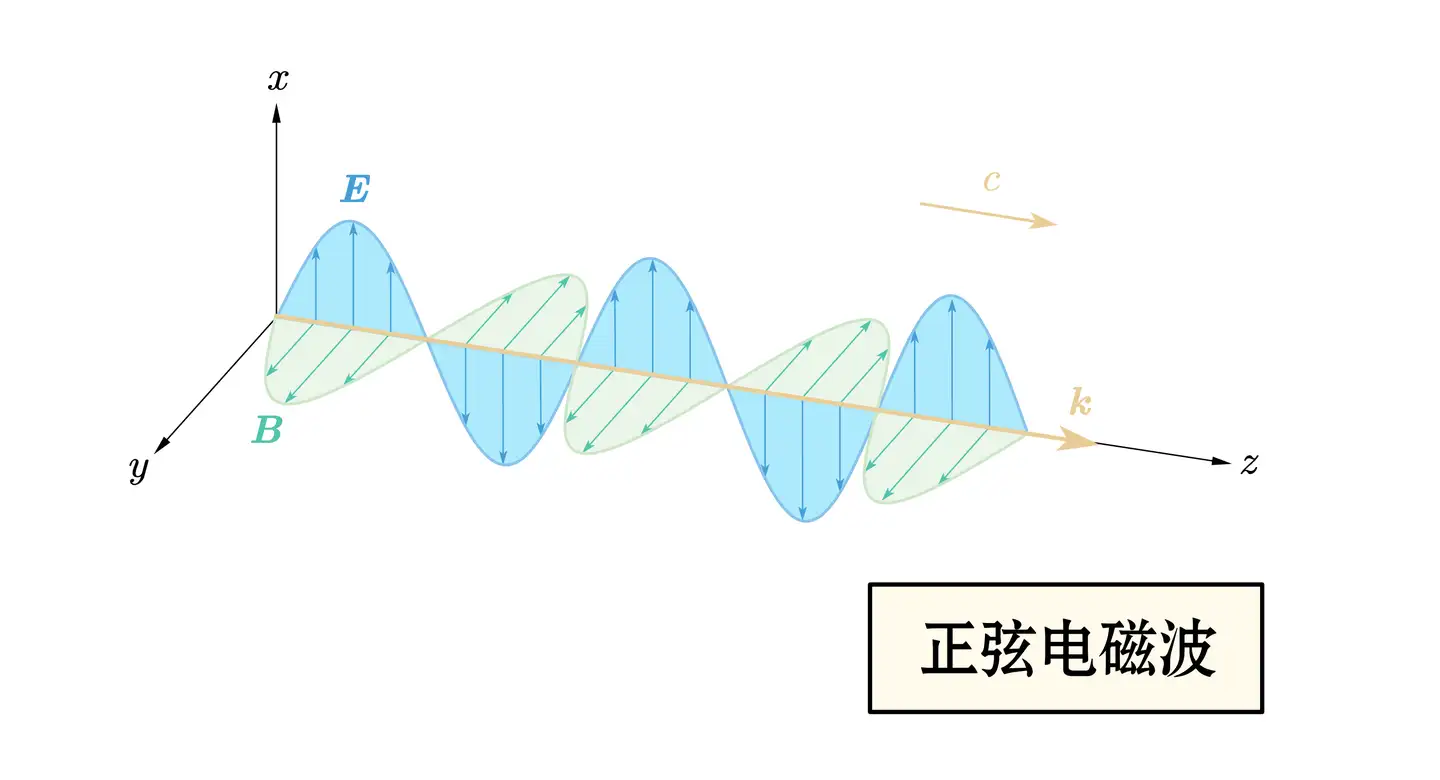
真空中电磁波传播的速度c=1μ0ϵ0就是光速,它的现代精确值是:
c=299792458m/s
——有时也会取成c=3×108m/s(每秒三亿米)。实际上,更准确的说法是这个光速的数值是我们规定的,我们拿它来定义长度单位“米”,换句话说以后就算对光速进行了更加精确的测定,要改变的也是“一米的长度”而不是光速的数值。
更进一步,人们发现了不同频率、各具作用的电磁波,它们本质上是相同的,只是频率ν和波长λ有着较大差别。按照波长从长到短(或者频率从低到高)的顺序排列,分别是无线电波、微波、红外线、可见光(红、橙、黄、绿、蓝、靛、紫)、紫外线、X射线和γ射线——这样的排列称为电磁波谱。这也说明了电磁波的“疆域”极其广阔,我们肉眼可见的光只是其中波长为400∼760 nm的很窄的一段,而我们的身边则到处在穿梭着更多的“不可见的光”,它们都满足λν=c的共同规律。
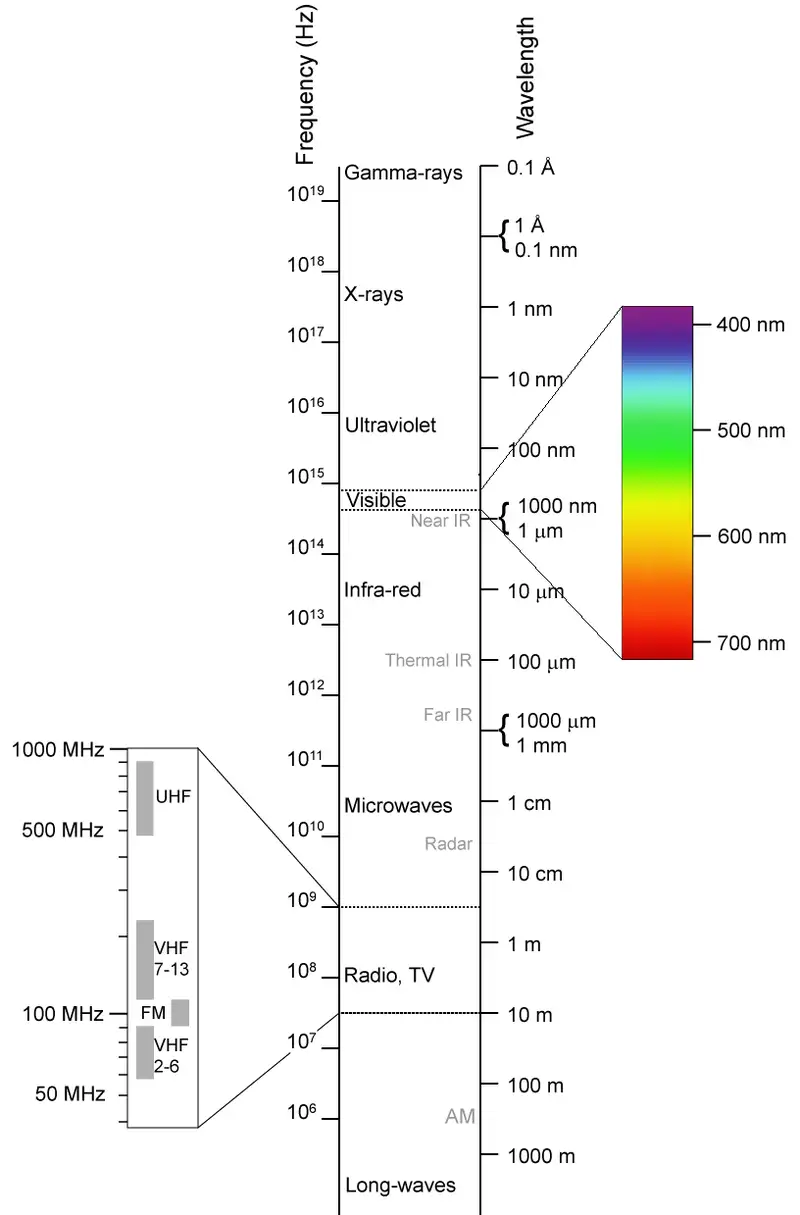
◆ 信息时代:浪潮之巅
麦克斯韦的伟大预言与赫兹的电火花,共同照亮了人类社会的发展道路。“电气时代”带来的改变还历历在目,而仅仅半个世纪后,电磁波的发现与应用,又为我们叩响了通向信息时代的大门。
信息是人们认识和改造世界的基础,我们每天都在接收和产生各种各样的信息。而信息的传递——通信,也是人类社会得以存在与发展的前提。为了让信息能够更快传递到更远的地方,自古以来人们就想尽了各式各样的办法——驿站快马、飞鸽传书、点燃烽火台、长跑马拉松…… 如果人类一直维持在古代社会,那么这些信息传递方式看上去似乎也够用了,然而进入19世纪的资本主义自由竞争时代后,大工业生产的发展、商品贸易的扩大、市场竞争的激烈、政治军事格局的瞬息万变等,让传统的通信模式已经无法适应社会发展的需要,人类迫切需要寻找全新的通信手段。恰好,赫兹实验发现的、能以光速携带信息传递的电磁波,就是我们要找的——最快的“信使”。
最开始尝试无线电通信的国家是俄国科学家波波夫,他早在1895年就制成了一台无线电接收机,1896年实现了无线通信,并成功传送了世界上第一封有实际内容的无线电报。而可悲的是,这项伟大的发明并没有得到当时沙皇俄国政府的重视,他们对用电磁波进行通信的“荒谬幻想”嗤之以鼻,不予拨款和支持。波波夫的贡献也因此被埋没,在47岁时因患脑溢血英年早逝。
不相信能用电磁波进行通信的人还有很多,其中甚至包括电磁波的发现者赫兹——他曾经说过,因为地球是圆的,所以“如果要利用电磁波进行无线通信,那非得有一面和欧洲大陆面积差不多的巨型反射镜才行。”但是“不信邪”的人也是存在的,尤其是年轻人。——1894年,一位刚从大学毕业的意大利青年马可尼也开始尝试研究无线通信,他比起波波夫来可要幸运得多,在他刚实现无线通信后不久就得到了英国邮电总局的支持,并创立了自己的公司。1899年,马可尼将无线电通信距离提升到了104公里。1901年,电磁波通信跨过了大西洋——人类的信息时代自此开篇。马可尼在1909年获得了诺贝尔物理学奖。同样可惜的是,赫兹早在1894年便已去世,并未能亲眼看到电磁波通信的光辉前景,而赫兹所疑惑的“巨型反射镜”后来被发现确实存在于天空之上,那就是大气里的电离层。
无线电通信之后,一个更加辉煌灿烂的时代来临了,人类社会就此被打上“信息化”的深刻印迹。电磁波通信的广泛应用让人们之间的信息联系加速了,使地球变得“更小”同时也“更活跃”。信息变成了联系经济、政治、科技活动以及人们家庭生活的有效介质,而信息特有的共享性更是成为了社会公平和均衡发展的基础,进一步强化了人们对世界整体性与动态性的理解。同时信息还塑造了人们生活、工作、学习、社交、休闲娱乐乃至战争的方式,创造了前所未有的社会财富,也给人类文明带来了前所未有的机遇与挑战。看看你的周围——广播、电视、雷达、导航、无线网和蓝牙,支撑我们现代生活的无数的现代技术都应用着电磁波,也都建立在电磁场理论的基础之上。
站在信息时代的浪潮之巅,展望着未来的“智慧世界”、“万物互联”,我们不会忘记这一切力量都蕴含在麦克斯韦的短短四行方程之中。当我们不管走到哪都要先问一句WIFI密码的时候,就应该意识到:电磁波在我们的生活里早已如同空气那样不可或缺了。
【三】电磁场与守恒律
◆ 电磁场的物质性
正如前文所言,在历史上,“近距作用”与“超距作用”的漫长争论始终伴随着电磁学发展的轨迹。从表面上来看,牛顿的万有引力定律是支持超距作用的,因此伴随着牛顿力学的成功,超距作用的观点也盛行起来,库仑定律、安培力定律等等都是本质上都是超距作用的观点在电磁学中的体现。然而,奥斯特、法拉第等人却从物理直观的角度,更相信自然界中不存在超距作用,电磁相互作用绝不是什么“瞬间隔空传递”,而是通过空气中弥漫的“力线”传播——这便是“场”概念的雏形。麦克斯韦所建立的电磁场理论,以及赫兹所发现的电磁波,证明了电磁相互作用是以一个有限的速度(即光速c)传递的,从此“超距作用”的观点在电磁学中终于被绝大多数物理学家抛弃了。
“近距作用”观点一统天下,作为物质另一种存在形态的“场”也必然受到关注。在“超距作用”的观点里,电磁相互作用必须以两个带电物体(电荷或电流)同时存在为前提,假如只有一个物体,即把“源”撤掉了,则一切相互作用也都不存在了。但在“近距作用”或者说法拉第场论的观点里,空间中存在着各种“力线”,而这些“力线”中携带着能量等,哪怕将“源”撤掉,只要“弾拨”这些“力线”,电磁相互作用照样会发生。于是,法拉第眼里的“场”已不再是为了方便计算力的大小而引入的数学工具,而是真实存在于空间里的物质。我们早已知道:电磁场本质上也是物质的一种形态,它的存在就和实物粒子的存在一样真实。电磁场理论将人类对物质的认识从有形的、集中的实物粒子过渡到无形的、弥散的场,标志着人类对物质世界的认识水平的重大前进。
电磁场既然同样是物质的一种,理所应当要和实物粒子构成的物质一样,携带着能量、动量与角动量。这样一来,电磁场和其他物质发生的所有相互作用,也必然要服从于能量守恒、动量守恒与角动量守恒的框架。而由于电磁场的全部规律已经在麦克斯韦方程组和洛伦兹力方程中得到体现,因此我们也可以猜想:这些守恒定律在电磁场中的具体形式也同样可以由麦克斯韦方程组推导出来。
在讨论这些守恒定律之前,让我们先回顾电荷守恒定律:
∂ρ∂t+∇⋅J=0
——非常清晰吧,我们完全可以把它当成是所有守恒定律的范例。(别忘了,它也不是独立规律,可以由麦克斯韦方程组直接导出。)接下来的问题便是:我们怎么把能量守恒、动量守恒和角动量守恒也写成相同的形式,也就是如何将电磁场中的“能量密度”、“动量密度”、“角动量密度”(相当于电荷密度ρ)以及“能量流密度”、“动量流密度”、“角动量流密度”(相当于电流密度J)表达出来。
◆ 电磁场的能量与能量守恒
电磁场有能量,这并不难理解。我们说“万物生长靠太阳”,太阳光便是一种电磁波,穿越茫茫宇宙向地球不断输送着光与热。阳光每分钟垂直照射到每平方厘米的地球表面上的能量约为8.2J,这些能量为地球带来了光明与温暖,是风能、水能、化学能、生物质能乃至地球上几乎一切能量的源泉。
要计算电磁场的能量,我们还是得从“功”的角度出发。假设我们有一定的电荷分布ρ与电流分布J,它们产生了电场E与磁场B。又经过一小段时间,电荷的分布发生了改变,那此时电荷总共受到了电磁场给它做的多少功呢?我们假定电磁力对电荷作用的总功率密度(即单位体积电荷所受的功率)为P¯,那么这种做功的实质是电磁场的能量传输给电荷,意味着电磁场中蕴含的能量随时间减少。我们把电磁场中蕴含的能量密度(单位体积内的能量)记作w,电磁场的能量流密度(简称能流密度,即单位体积内通过截面上的单位面积流出的能量)记作S,仿照电荷守恒定律,我们也能写出电磁场能量守恒定律的微分形式:
∂w∂t+∇⋅S=−P¯
——如果写成−∂w∂t=P¯+∇⋅S或许会更好理解一点:某个区域内电磁场里蕴含的能量如果减少了,只有两种原因,一是通过边界面流出了本区域,二是以电磁力做功的方式传输给了电荷(变成了电荷运动的机械能)。这里的w就类似ρ,而S就类似J。接下来我们要做的是求出其中w、S、P¯的具体形式。
计算P¯并不难,利用洛伦兹力公式,要注意磁力不做功,所以真正纳入考虑的仅仅是电场力。
P¯=f¯⋅v=(ρE+J×B)⋅v=E⋅ρv=E⋅J
接下来要做的是将这个“总功率密度”E⋅J只用电场和磁场表示出来,以尽可能“凑出”上面能量守恒定律的形式。我们立刻就能想到安培定理(即麦克斯韦方程组里的第四行∇×B=μ0J+μ0ϵ0∂E∂t)。代入后,方程变为:
P¯=E⋅J=E⋅(1μ0∇×B−ϵ0∂E∂t)
利用矢量公式∇⋅(E×B)=B⋅(∇×E)−E⋅(∇×B)以及法拉第定律∇×E=−∂B∂t,又可以写为:
P¯=−∇⋅(1μ0E×B)−(ϵ0E⋅∂E∂t+1μ0B⋅∂B∂t)
整理后得到:
∂∂t12(ϵ0E2+1μ0B2)+∇⋅1μ0(E×B)=P¯
对照上面的能量守恒方程,则电磁场的能量密度w与能流密度S的表达式分别写为:
{w=12(ϵ0E2+1μ0B2)S=1μ0(E×B)
就可以还原出能量守恒定律的形式:
∂w∂t+∇⋅S=−P¯
——也就是说,每单位体积的电磁场存储了12(ϵ0E2+1μ0B2)的电磁能,电磁波在垂直于传输方向的每单位面积上可以流过(传输)1μ0(E×B)的电磁能,所以电磁波的传播是必定携带能量的。
电磁能密度w从直观上就可以分为“电能密度”12ϵ0E2和“磁能密度”12μ0B2两部分,熟悉电磁学的小伙伴很快能就发现它们其实是静电场中的电能(例如电容器12CU2)和静磁场中的磁能(例如电感线圈12LI2)除以体积后的微分形式——我们再一次见到了这种用“平方关系”表述的能量形式!能流密度矢量S有时也称作坡印廷矢量,相应地上述电磁场能量守恒关系式也被叫做坡印廷定理。
——我们可以看出:能量守恒其实是麦克斯韦方程组和洛伦兹力公式的必然推论,因此电磁场的基本规律本身就蕴含了能量守恒的成立。于是,电磁场本身就蕴含了能量,能量可以在场的不同地方转移,也可以与带电体(电荷、电流)等的其他形式能量(机械能等)彼此转换,当我们将电磁场本身的能量纳入考虑时,电磁相互作用中能量守恒也是成立的!这一结论进一步说明了电磁场绝不仅仅是一种数学描述手段,而是实在的物理客体。当带电体能量减少时,一定是电磁波带走了能量;反之带电体的能量增加也可能是吸收了电磁波送来的能量。如果大胆一点,用w′表示带电体的机械能密度,则它和场的电磁能密度w加起来就成为了这片区域的总能量密度,能量守恒也可以写成如下更漂亮的形式:
∂∂t(w+w′)+∇⋅S=0
◆ 电磁场的动量与动量守恒
电磁场既然是一种物质,那么它除了带有能量,还应该带有动量。如果电磁波(光)带有动量,那么被照射到的物体就会感受到压强(辐射压,或称为光压),麦克斯韦曾计算出晴天的阳光对地面的压强大约为5×10−6Pa——这么小的压强显然只能用精密仪器才能测出,难怪此前的人们一直没有发现,直到1901年才由俄国物理学家列别捷夫首次用实验证实。然而,在极大的天体物理尺度或者极小的粒子物理尺度,辐射压的影响将会非常明显,人们甚至已经开始设想不耗费任何燃料、直接用太阳的光压推动宇宙飞船的“光帆”。
我们很容易认定:在电磁相互作用里,动量守恒也是应当成立的。为此我们可以仿照上面的能量守恒,列出动量守恒的关系式。只需把能量密度w换成“动量密度”、能流密度S换成“动量流密度”、单位体积内电磁力对带电体做功的功率P¯换成单位体积内电磁力对带电体施加冲量的速率——这显然就是力,因此它就是单位体积的电荷受到的洛伦兹力f¯罢了。不过与之前不同的是,这回的动量是矢量,所以动量密度也是矢量,用g表示;动量流密度就必须是一个二阶张量了,用T表示。直接仿照上面的能量守恒,不难写出电磁场里动量守恒定律的形式应为:
∂g∂t+∇⋅T=−f¯
——接下来要干的事情便很明确了,一样是把g和T的具体形式用场表达出来。
首先,f¯=ρE+J×B是人尽皆知的。根据麦克斯韦方程组里的第一行(高斯定理∇⋅E=ρ/ϵ0)和第四行(安培定理∇×B=μ0J+μ0ϵ0∂E∂t),可将洛伦兹力里面的ρ和J直接换掉,改写为:
f¯=ϵ0(∇⋅E)E+(1μ0∇×B−ϵ0∂E∂t)×B
——这个式子看上去没什么头绪,但此时还有两个尚未用到的方程(法拉第定律∇×E=−∂B∂t、高斯磁定理∇⋅B=0)。发挥我们的聪明才智,可以将这两个方程“组装”成如下的辅助关系式:
0=1μ0(∇⋅B)B+ϵ0(∇×E+∂B∂t)×E
两式相加,我们能得到一个关于E和B看上去很“对称”的形式:
不带时间微商,只与相关的两项不带时间微商,只与相关的两项带时间微商的两项f¯=ϵ0(∇⋅E)E+(1μ0∇×B−ϵ0∂E∂t)×B+1μ0(∇⋅B)B+ϵ0(∇×E+∂B∂t)×E=ϵ0(∇⋅E)E+ϵ0(∇×E)×E⏟不带时间微商,只与E相关的两项+1μ0(∇⋅B)B+1μ0(∇×B)×B⏟不带时间微商,只与B相关的两项+ϵ0∂B∂t×E−ϵ0∂E∂t×B⏟带时间微商的两项
——可以发现,最终的结果一共有六项,而且其中带时间微商的只有两项!在剩下的四项里,又有两项只和E有关,剩下两项只和B有关。很容易猜想:这带时间微商的两项就会是最后的∂g∂t,而剩下的四项就会是最后的∇⋅T(当然会差一个负号)。条理清晰多了!接下来就是逐个击破。
对于带时间微商的两项,很容易合并出:
ϵ0∂B∂t×E−ϵ0∂E∂t×B=−ϵ0(E×∂B∂t+∂E∂t×B)=−∂∂t(ϵ0E×B)
对于不带时间微商的四项,由于电场两项和磁场两项完全对称,以电场两项为例,根据矢量公式(∇×E)×E=(E⋅∇)E−12∇E2,可以写出:
ϵ0(∇⋅E)E+ϵ0(∇×E)×E=ϵ0(∇⋅E)E+ϵ0(E⋅∇)E−12ϵ0∇E2=ϵ0∇⋅(EE−12E21)
——这样做就成功把这一项表达成了一个二阶张量散度的形式(其中EE显然是并矢的写法,而1代表单位二阶张量)。同理,对于磁场的那两项,我们用一模一样的方法:
1μ0(∇⋅B)B+1μ0(∇×B)×B=1μ0(∇⋅B)B+1μ0(B⋅∇)B−12μ0∇B2=1μ0∇⋅(BB−12B21)
最终,我们便将动量守恒的整个式子改造为:
∂∂t(ϵ0E×B)+∇⋅[12(ϵ0E2+1μ0B2)1−ϵ0EE−1μ0BB]=−f¯
所以,当电磁场的动量密度g与动量流密度T只要分别写成:
{g=ϵ0E×BT=12(ϵ0E2+1μ0B2)1−ϵ0EE−1μ0BB
便能得到最终的动量守恒形式:
∂g∂t+∇⋅T=−f¯
与之前同理,如果也计入带电体的机械动量密度g′,便可得出包括带电体和电磁场在内的总动量守恒表达式:
∂(g+g′)∂t+∇⋅T=0
如果再将之前能量密度w和能流密度S的式子代入,我们还能得到关于动量密度g与动量流密度T的更简洁表达形式:
{g=c2ST=w1−ϵ0EE−1μ0BB
“动量密度”g相对来说比较好理解,那么“动量流密度”T又是什么意思呢?如果我们将电磁场看作一种像弹性体或流体般的连续介质,那么所谓的“动量流密度”本质描绘的是不同方向上的单位面积在单位时间内通过的通量(即受力),可见它本身所表征的就类似于之前我们所知的应力的概念!没错,只需将T前面添一个负号(因为描述应力时常以受拉为正,而这里的动量流密度却是以电磁场的动量流出为正,对带电体来说便相当于动量的流入,即带电体受压),所得到的−T既是描绘带电体所受电磁场应力的张量,即所谓麦克斯韦应力张量。——当然,有的书上也会直接用T来表示麦克斯韦应力张量,而用−T表示电磁场的动量流密度张量。
麦克斯韦应力张量的形式是:
−T=[ϵ0(Ex2−E2/2)+1μ0(Bx2−B2/2)ϵ0ExEy+1μ0BxByϵ0ExEz+1μ0BxBzϵ0ExEy+1μ0BxByϵ0(Ey2−E2/2)+1μ0(By2−B2/2)ϵ0EyEz+1μ0ByBzϵ0ExEz+1μ0BxBzϵ0EyEz+1μ0ByBzϵ0(Ez2−E2/2)+1μ0(Bz2−B2/2)]
——它为我们提供了另一种计算带电体所受电磁场作用力的方法。如果说利用洛伦兹力公式属于“微观形式”的话,那么利用带电体周围的电磁场直接计算电磁场应力,当属“宏观形式”。
最后需要说明的是:在涉及到电磁场的一些力学问题中,你经常会遇到“牛顿第三定律好像失效了”的困惑。其实我们知道,牛顿第三定律在力学中之所以能成立,归根到底是由动量守恒保证的。但如果这里面还涉及到机械动量和电磁场动量的转化,即使动量守恒永远成立,但如果用牛顿第三定律,便会“算漏了场的动量”,所以牛顿第三定律才会失效。由此可见,牛顿第三定律其实并不是普遍成立的规律,而是只在一定条件下成立的近似规律。我们知道日常生活中遇到的绝大部分力(弹力、支持力、摩擦力等等)都属于电磁力,仅仅只是因为这些力作用的物体都呈现宏观电中性,所以电磁作用力只有在相互接触的时候才能表现出来,电磁场的变化微不足道,所以我们才能近似适用牛顿第三定律。但无论如何,动量守恒才是比牛顿第三定律更普遍的基本规律。
◆ 电磁场的角动量与角动量守恒
同样的道理,作为一种物质的电磁场还具备角动量。如果我们用位矢x去叉乘动量守恒式,将得到:
∂(x×g)∂t+x×(∇⋅T)=−x×f¯
右边的−x×f¯无疑便是单位体积电磁力所提供的力矩,现在我们只需要将x×∇⋅T改写为散度形式。这里需要利用另一个矢量公式x×(∇⋅T)=−∇⋅(T×x)(该公式的成立依赖于T是对称张量,可以尝试使用前面所说的δ符号与ε符号证明),便可以写成:
∂(x×g)∂t+∇⋅(−T×x)=−x×f¯
于是,电磁场的角动量密度矢量(用l表示)和角动量流密度张量(用R表示)便能写为:
{l=x×gR=−T×x
角动量守恒的关系式写作:
∂l∂t+∇⋅R=−x×f¯
——如果也计入带电体的角动量…… 后面的结论你肯定信手拈来了。
至此,我们彻底证明了:电磁场和其他物质一样,同样具备能量、动量和角动量,所有和电磁场有关的相互作用过程同样要服从能量守恒、动量守恒与角动量守恒定律。在我们运用这些守恒定律时,请务必注意:不要忘记考虑场所携带的能量、动量或角动量!这一切都说明了“电磁场是一种物质”的本性。
◆ 电磁单位制
在本篇的最后,我们需要花一点篇幅捋清楚电磁学里纷繁复杂的单位制。这是因为电磁单位制因为历史原因多达十几种,而各种书籍、文献在选用单位制时常常自行其是、各不相同,容易产生困惑。考虑到最常用的还是国际单位制和高斯单位制两种,我们最好还是同时掌握这两种单位制的概念与转换,以作为应付这一既成事实的权宜之计。
国际单位制(SI)是大家最熟悉的,也是国际与中国都推荐采用的标准单位制。在力学中,国际单位制选择了三个基本物理量——长度、质量、时间,并分别采用米(m)、千克(kg)、秒(s)作为基本单位。进入电磁学,原则上只需要再添加一个基本物理量就够用了(选择电荷、电流、电势、电场等等都是可以的),其他的电磁学量都能用它来推导出来。最终选定了电流作为基本物理量,采用安培(A)作为基本单位,这无疑和当时电路科学的迅猛发展有关。这样一来,国际单位制下电荷的单位(库仑,C)便需要用电流乘以时间导出(即1 C=1 A⋅s)。
另一种力学单位制被称为厘米-克-秒制(CGS),顾名思义,它尽管同样选择长度、质量和时间作为力学领域的基本物理量,但采用的基本单位却分别是厘米(cm)、克(g)、秒(s)。这会导致由此定义的其他力学单位与国际单位制里对应的单位存在换算倍率的差异,例如厘米-克-秒制中定义的力的单位为“达因”(1 dyn=1 g⋅cm/s2),1达因等于10−5牛顿;能量的单位为“尔格”(1 erg=1 g⋅cm2/s2),1尔格等于10−7焦耳;压强的单位为“巴”(1 Bar=1 dyn/cm2),1巴等于105帕等等。如今,在一些老教材里,你或许还能看见厘米-克-秒制单位的踪迹。
如果说厘米-克-秒制的力学单位还仅仅是换算倍率的差异,一旦它进入电磁学,便会面临究极的混乱——一个首要的问题是:到底要不要选择新的基本物理量?当时的一种思路是不额外选择电磁学的基本物理量,而只是根据电磁学的公式去直接得到电磁学量的单位表示。接下来的问题:选择哪个电磁学公式作为基础?一派选择的是描述电荷受力的库仑定律,规定库仑力F=kCqq′r2里的常量kC=1,由此规定的电荷单位称为“静电库仑”或“富兰克林”(1 Fr=1cm⋅dyn),这样电流就是电荷的衍生(电流单位为Fr/s),这种单位制称作静电单位制(ESU)。另一派则选择描述电流受力的安培力定律,规定安培力dF=kAII′dldl′r2里的常量kA=1,由此规定的电流单位称为“绝对安培”或“毕奥”(1 Bi=1 dyn),这样电荷成了电流的衍生(电荷单位为Bi⋅s),这种单位制称作电磁单位制(EMU)。——无论是用这两种单位制里的哪种,它们的共同特点是:电荷和电流都没有独立的量纲。
将厘米-克-秒制里的静电单位制和电磁单位制“混搭”在一起(电学量采用静电单位制,磁学量采用电磁单位制),就变成了电磁学教科书里比较常见的高斯单位制(GSU)。具体来说,在高斯单位制里,电荷、电流、电场、电势等全部采用静电单位制中的定义,而磁场、磁矩、磁通量等采用电磁单位制里的定义,磁场的单位为“高斯”(1 Gs=1 dyn/(Bi⋅cm)),1高斯等于10−4特斯拉。因为“电流”这个关键的物理量依从了静电单位制,所以高斯单位制里的kC=1,而kA=1/c。
——单位制的不同会导致很显著的差别,例如用不同的单位制表达出的电磁学公式的形式会是不同的!让我们对比一下利用国际单位制(左)和高斯单位制(右)分别表示的麦克斯韦方程组:
{∇⋅E=ρϵ0∇×E=−∂B∂t∇⋅B=0∇×B=μ0J+μ0ϵ0∂E∂t {∇⋅E=4πρ∇×E=−1c∂B∂t∇⋅B=0∇×B=4πcJ+1c∂E∂t
以及利用国际单位制(左)和高斯单位制(右)分别表示的洛伦兹力公式、库仑(场)定律、毕奥-萨伐尔定律、标势与矢势,还有能量密度与能流密度:
{F=q(E+v×B)E=14πϵ0∫1r2erdq′B=μ04π∫Idl′×err2E=−∇φ−∂A∂tB=∇×Aw=12(ϵ0E2+1μ0B2)S=1μ0(E×B) {F=q(E+1cv×B)E=∫1r2erdq′B=1c∫Idl′×err2E=−∇φ−1c∂A∂tB=∇×Aw=18π(E2+B2)S=c4π(E×B)
——相比起来,你能发现的最大的变化便是方程的系数有所不同。在国际制里像“牛皮癣”一样到处可见的常数ϵ0和μ0在高斯制里消失了(也就是说在高斯制里认为ϵ0=μ0=1),这确实让方程的形式得到了简化——但代价是高斯制的公式里多出了很多c。而且我们会发现:在高斯制里电场E和磁场B居然拥有相同的量纲。除此之外,国际单位制与高斯单位制之间的转化会导致“有理”与“无理”的性质发生逆转——原本不含有4π因子的公式(例如麦克斯韦方程组等)变成含有4π因子,而原本含有4π因子的公式(例如库仑定律、毕奥-萨伐尔定律等)变成不含4π因子。
这些不同的单位制之间可以进行转换,当然最省事的方法绝不是死记硬背各种转换因子,而是查表。随着时代的变迁,国际单位制渐成主流,但是在少数领域依然沿袭习惯(例如部分电磁学领域采用高斯单位制、基础理论物理采用自然单位制等等,这里必须点名反人类的英制单位……早该废掉了)。在本专栏中,若无特殊说明,均采用和国家法定标准一致的国际单位制。
“在每一学科领域都有一些特殊的个人,他们似乎具有天赐之福,他们放射出一种超越国界的影响,直接鼓舞和促进着全世界去探求。詹姆斯·克拉克·麦克斯韦是他们当中屈指可数的一位。”本篇之中,我们回顾了麦克斯韦电磁场理论的建立历程。当麦克斯韦用它简洁的四行方程组去概括电磁场的规律,当赫兹在麦克斯韦预言的指引下发现电磁波时,利用电磁波创造人类共同福祉的宏伟时代随之呼啸而来。
与此同时,麦克斯韦对电磁场的物质性的深刻洞见,特别是发现电磁场也具有能量、动量、角动量等属性,对物理实在观念的发展有着重大影响,爱因斯坦说过:“相信有一个离开知觉主体而独立的外在世界,是一切自然科学的基础。”(是不是很像关于唯物主义的论述呢?)然而,在曾经的牛顿经典力学观念里,“物理实在”是由质点去代表的,质点是“物质”的唯一形式,任何物质都要被解释成质点,这也是机械论的观点,但麦克斯韦却证实了:有那么一种“物理实在”并不能用质点来表示,而是以空间中连续的场的形式存在的!这是物理学自牛顿以来的一次最深刻的思想变革,因此爱因斯坦曾评述道:
“自从牛顿奠定理论物理学的基础以来,物理学的公理基础——换句话说,就是我们关于实在的结构的概念——的最伟大的变革,是由法拉第和麦克斯韦在电磁现象方面的工作而引起的。”
量子论的创立者普朗克更是指出:
“麦克斯韦的名字将永远镌刻在经典物理学家的门扉上,永放光芒。从出生地来说,他属于爱丁堡;从个性来说,他属于剑桥大学;从功绩来说,他属于全世界。”
——麦克斯韦方程组还为我们留下了最后一个“彩蛋”。我们早已知道,按照从麦克斯韦方程组推导出的结论,真空中的光速是:
c=1μ0ϵ0
——它是常量,这个光速的结论普遍适用于一切电磁波。但这下产生了一件诡异的事情:在我们的推导过程中根本没有涉及到任何特定参考系的指定!而我们知道,参考系变了速度就要变,假如不指定清楚参考系,那么这个速度是没有意义的。
所以……
究竟是光只能相对于某个特定的参考系的速度为c=1/μ0ϵ0呢……
还是说,光相对于任何参考系的速度都是c=1/μ0ϵ0呢?
……!!!
欲知后事如何,请听下回分解~ ^_^
