拉普拉斯算子

https://zhuanlan.zhihu.com/p/376436061

18世纪下半叶到19世纪中叶可以说是法国众星璀璨的辉煌时代，彼时彼刻，拿破仑当政，重视科研与教育，涌现出一大批杰出的科学家。众星闪耀，50年后，72个名字刻上了艾菲尔铁塔，拉普拉斯（Laplace, 1749 – 1827）和泊松（Poisson, 1781 – 1840）在列。以拉普拉斯命名的数学名词有一些[1]，最出名的当属拉普拉斯方程和拉普拉斯变换。本文主要阐述拉普拉斯方程相关的知识和推导。

拉普拉斯（Laplace, 1749 – 1827）

　　拉普拉斯方程[2]是二阶偏微分方程，对于n维空间的标量函数 f(x_1, x_2, …, x_n) 有
\nabla ^2 f = \frac {\partial ^2 f}{\partial x_1^2} + \frac {\partial ^2 f}{\partial x_2^2} + … + \frac {\partial ^2 f}{\partial x_n^2} = 0。

为了方便，引入符号 \Delta = \nabla \cdot \nabla = \nabla ^2 。

\nabla ^2 f = \frac {\partial ^2 f}{\partial x_1^2} + \frac {\partial ^2 f}{\partial x_2^2} + ... + \frac {\partial ^2 f}{\partial x_n^2} = 0。为了方便，引入符号 \Delta = \nabla \cdot \nabla = \nabla ^2

这里 \Delta 是拉普拉斯算子，定义为梯度（gradient）的散度（divergence）。 \Delta 也用作微小增量符号、一元二次方程的判别式符号，不要搞混了。\nabla \cdot 是散度记号，字母符号是 div。 \nabla 是梯度记号，字母符号记作 grad[3]。div(grad(f)) = 0。

　　求解拉普拉斯方程是电磁学、天文学、热力学和流体力学等领域经常会遇到的一类重要的数学问题，因为这类方程以势函数 \varphi (x, y, z) 的形式描写电场、引力场和流场等物理对象（一般统称为保守场或有势场）的性质。

　　满足拉普拉斯方程的函数叫调和函数、谐函数、谐和函数（harmonic function）。谐来源于绷紧的弦的振动，即简谐运动（Simple harmonic motion），该类微分方程的解为正弦函数和余弦函数的线性叠加。周期函数可以通过傅里叶级数展开为常数（即直流分量）与一组具有共同周期的正弦函数、余弦函数（交流分量）之和。谐波频率是基波频率 f 的整倍数，基波频率 N 倍的正弦波称之为 N 次谐波。谐也通用于音乐理论之中。乐器振动发出不同倍数频率的声音，频率最低的称为基音，频率成整数倍的音是泛音，基音和泛音统称谐音。

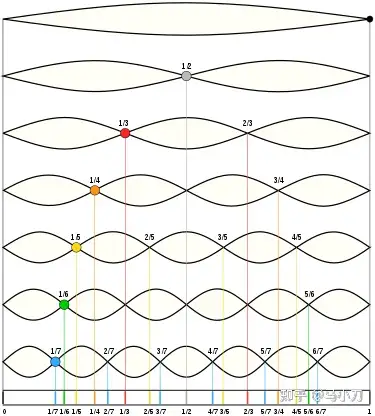
绳子抖动的模式是谐波

一维解

\nabla ^2 f = \frac {d ^2 f}{d x^2} = 0 ，只有一个未知数，所以这里用了导数符号d，而不是偏导数符号 \partial 。一维解很简单。 函数的二阶导数为0，则一阶导数为常数，所求函数为一次函数，于是通解为 f(x) = a x + b ，a和b为常数。两点确定一条直线。除去 a = 0 时的常量情况 f(x) = b，该函数为单调递增或单调递减的线性函数。

\begin{align} \frac {d^2 f}{d x^2} &= \lim \limits_{a \to 0} \frac {f'(x) – f'(x – a)} {a} \\ &= \lim \limits_{a \to 0} \frac {[f(x + a) – f(x)]/a – [f(x) – f(x – a)]/a} {a} \\ &= \lim \limits_{a \to 0} \frac {f(x + a) – 2f(x) + f(x – a)} {a^2} \\ \end{align}

\begin{align} \frac {d^2 f}{d x^2} &= \lim \limits_{a \to 0} \frac {f'(x) - f'(x - a)} {a} \\ &= \lim \limits_{a \to 0} \frac {[f(x + a) - f(x)]/a - [f(x) - f(x - a)]/a} {a} \\ &= \lim \limits_{a \to 0} \frac {f(x + a) - 2f(x) + f(x - a)} {a^2} \\ \end{align}

　　如果二阶导数存在，此处极限的分子、分母近乎 0。拐点（ inflection point ）是曲线的凹凸分界点，该点处的二阶导数为 0。反之不成立，对于线性函数 f(x)，处处满足 f”(x) = 0，但没有拐点。

　　线性函数有性质 f(x) = \frac {f(x + a) + f(x -a)}{2} 。二维空间里的线，三维空间里的面，递推到n维空间里的超平面（Hyperplane），都有这种性质——函数在任意点的值，等于该点左右、前后、上下等共2n个等距离点所取值的平均值。
学过数字图像处理课程的，都知道离散形式的拉普拉斯算子——
一个3×3的矩阵 \begin {bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \\ \end {bmatrix} 。

 \begin {bmatrix} 0 & 1 & 0 \\ 1 & -4 & 1 \\ 0 & 1 & 0 \\ \end {bmatrix}

二维解

\nabla ^2 f = \frac {\partial ^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2} = 0 ，

\nabla ^2 f = \frac {\partial ^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2} = 0

看看特殊情况下函数 f(x, y) 的二维解。假设 x 和 y 相互独立，则有常数关系 \frac {\partial ^2 f}{\partial x^2} = -\frac {\partial ^2 f}{\partial y^2} = 2 a ，

 \frac {\partial ^2 f}{\partial x^2} = -\frac {\partial ^2 f}{\partial y^2} = 2 a

其中 2a 为任意常数，对于单独的 x 有 X(x) = a x^2 + b_1 x + c_1，对单独的 y 亦有 Y(y) = -a y^2 + b_2 y + c_2。由于相互独立，可以取两者之和： f(x, y) = X(x) + Y(y) = a(x^2 – y^2) + b_1 x + b_2 y + c_1 + c_2 ，

 f(x, y) = X(x) + Y(y) = a(x^2 - y^2) + b_1 x + b_2 y + c_1 + c_2 

 c_1 和 c_2 两个常数可合并，得到二维下的一种解 f(x, y) = a(x^2 – y^2) + b_1 x + b_2 y + c 。

 f(x, y) = a(x^2 - y^2) + b_1 x + b_2 y + c 

取两者之和是一种解题思想。满足 \frac {\partial ^2 f}{\partial x \partial y} = 0 

 \frac {\partial ^2 f}{\partial x \partial y} = 0

的函数有很多，只要能将 f(x, y) 拆分成关于 x 的函数与关于 y 的函数的和，都是解。f(x, y) = X(x) + Y(y)，先对 x 求偏导，丢掉 \frac {\partial Y}{\partial x} = 0 

 \frac {\partial Y}{\partial x} = 0

得到关于 x 的式子 \frac {\partial X}{\partial x} ，再对 y 求偏导，也成了常数而被丢弃。先对 y 求偏导再对 x 求偏导也一样， \frac {\partial X}{\partial y} = 0 。

 \frac {\partial X}{\partial y} = 0

　　前面的式子 f_1(x) = a x^2 + b_1 x + c_1 系数，我们用的是“真”常数，考虑到在偏微分中，异于自己的变量也算常数，即对变化的 x 来讲，y、sin(2y)、ln(3y)……都算常数。代入第一个， X(x) = x^2y + b_1 xy + c_1 和 Y(y) = -x y^2 + b_2 xy + c_2 得， f(x, y) = kxy + c 也是一种解。k、c为常数。

　　这里提一下泊松方程 \nabla ^2 \varphi = f ，

\nabla ^2 \varphi = f 

在拉普拉斯方程的基础上，右端的 0 换成了函数。或者说，拉普拉斯方程是它的特别案例，函数 f = 0。考虑方程 \nabla ^2 f = k ，k为常数，如法炮制解得 f(x, y) = a x^2 + (\frac k 2 – a)y^2 + b_1 x + b_2 y + c 。函数图像是二次曲线，拉普拉斯方程的这种解是双曲抛物面，因形似马鞍，也叫马鞍面。泊松方程的解可以是椭圆抛物面。

相比二阶线性偏微分方程的一般式

 A \frac {\partial ^2 f}{\partial x^2} + 2B \frac {\partial ^2 f}{\partial x \partial y} + C \frac {\partial ^2 f}{\partial y^2} + D \frac {\partial f}{\partial x} + E \frac {\partial f}{\partial y} + F f + G = 0 

A \frac {\partial ^2 f}{\partial x^2} + 2B \frac {\partial ^2 f}{\partial x \partial y} + C \frac {\partial ^2 f}{\partial y^2} + D \frac {\partial f}{\partial x} + E \frac {\partial f}{\partial y} + F f + G = 0 

而言，没有 \frac {\partial ^2 f}{\partial x \partial y} 项。

 \frac {\partial ^2 f}{\partial x \partial y}

对于满足 \frac {\partial ^2 f}{\partial x^2} \cdot \frac {\partial ^2 f}{\partial y^2} – \big( \frac {\partial ^2 f}{\partial x \partial y} \big)^2 < 0

 \frac {\partial ^2 f}{\partial x^2} \cdot \frac {\partial ^2 f}{\partial y^2} - \big( \frac {\partial ^2 f}{\partial x \partial y} \big)^2 < 0 

 的函数有马鞍点。代入上式值为 -4a^2 ，a 不为 0 时 -4a^2 < 0 为马鞍面，否则退化成平面。

　　以上是加法关系，我们来看看乘法关系。

假设函数是变量可分离的[4]，有 f(x, y) = X(x) \cdot Y(y) 。f 对 x 求偏导，则 Y(y) 相当于常数，直接提取出来为系数， \frac {\partial ^2 f}{\partial x^2}= Y \frac {\partial ^2 X}{\partial x^2} 。

有 f(x, y) = X(x) \cdot Y(y) 。f 对 x 求偏导，则 Y(y) 相当于常数，

\frac {\partial ^2 f}{\partial x^2}= Y \frac {\partial ^2 X}{\partial x^2}

对 y 同理有 \frac {\partial ^2 f}{\partial y^2}= X \frac {\partial ^2 Y}{\partial y^2} 。代入得 Y \frac {\partial ^2 X} {\partial x^2} + X \frac {\partial ^2 Y}{\partial y^2} = 0 。

 \frac {\partial ^2 f}{\partial y^2}= X \frac {\partial ^2 Y}{\partial y^2} 。代入得 Y \frac {\partial ^2 X} {\partial x^2} + X \frac {\partial ^2 Y}{\partial y^2} = 0

两边同时除以 XY，也就是除以 f(x, y)，得到 \frac 1 X \frac {\partial ^2 X}{\partial x^2} + \frac 1 Y \frac {\partial ^2 Y}{\partial y^2} = 0。

 \frac 1 X \frac {\partial ^2 X}{\partial x^2} + \frac 1 Y \frac {\partial ^2 Y}{\partial y^2} = 0

此处要求除数 f(x, y) 不恒为0，f(x, y) = 0 当然是一个解，撇开后可以做除法。由于两项相互独立，前者只与x有关，后者只与 y有关，考虑到 x、y是任意变化的，只可能两项均为常数。从而得到方程 \frac 1 X \frac {\partial ^2 X}{\partial x^2} = k^2 ， \frac 1 Y \frac {\partial ^2 Y}{\partial y^2} = -k^2 ，

从而得到方程 \frac 1 X \frac {\partial ^2 X}{\partial x^2} = k^2 ， \frac 1 Y \frac {\partial ^2 Y}{\partial y^2} = -k^2 

归为两个二阶常系数齐次线性微分方程的求解[5]，有公式可套。一正一负，X 和 Y 可轮换。这里用了常数 k^2 ，方便后面开方。

　　二阶常系数齐次线性微分方程 y″ + py′ + qy = 0 的特征方程（characteristic equation）为 r^2 + p\,r + q = 0。若有两根 α 和 β ，则通解为 y = c_1 e^{\alpha x} + c_2 e^{\beta x} ；若有重复的根 α ，则通解为 y = (c_1 + c_2 x)\, e^{\alpha x}；若无实数根，虚数根为 \alpha \pm \beta i ，则通解为 y = e^{\alpha x}(c_1 \cos (\beta x) + c_2 \sin (\beta x))\, 。其中 c_1 和 c_2 为常数。

\frac {\partial ^2 X}{\partial x^2} – k^2 X = 0 的特征方程有两个实根 \pm k ，解为 X(x) = c_1 e^{kx} + c_2 e^{-kx} 。此解也可以写成双曲函数形式，等同于 X(x) = (c_1 + c_2) \sinh (kx) + (c_1 – c_2) \cosh (kx) ，其中双曲正弦 \sinh (kx) = \frac {e^{kx} – e^{-kx}} 2 ，双曲余弦 \cosh (kx) = \frac {e^{kx} + e^{-kx}} 2 。所以解也写成 X(x) = c_1 \cosh (kx) + c_2 \sinh (kx) ，跟下面要说的解形式一样。

\frac {\partial ^2 Y}{\partial y^2} + k^2 Y = 0 的特征方程有两个虚根 \pm k i ，解为 Y(y) = c_3 \cos (ky) + c_4 \sin (ky) 。

乘在一起得到第三种解 f(x, y) = (c_1 e^{kx} + c_2 e^{-kx})\, (c_3 \cos (ky) + c_4 \sin (ky)) 。上面说过 X 和 Y 可轮换，所以 f(x, y) = (c_1 \cos (kx) + c_2 \sin (kx))\, (c_3 e^{ky} + c_4 e^{-ky}) 也可以。

 f(x, y) = (c_1 e^{kx} + c_2 e^{-kx})\, (c_3 \cos (ky) + c_4 \sin (ky)) 。

上面说过 X 和 Y 可轮换，
所以 f(x, y) = (c_1 \cos (kx) + c_2 \sin (kx))\, (c_3 e^{ky} + c_4 e^{-ky}) 也可以。

　　以上仅列举了几种形式的解，它们之间的线性组合也都算解，这个是线性系统的性质，叫叠加原理（Superposition principle）。拉普拉斯方程的解包括这些，但不限于这些。因为没有给定边界条件，所以解是不确定的。

唯一性定理

　　唯一性定理（The Uniqueness Theorem[6]）给出了确定保守场的条件，为求保守场的势函数指明了方向。更重要的是，它具有十分重要的实用价值。无论你采用什么方法得到的解，哪怕是七拼八凑弄到了方程的一个解，只要该解满足泊松方程和给定的边界条件，那么该解就是唯一的正确解。因此对于许多具有对称性的问题，可以不必用繁杂的数学去求解泊松方程，而是通过提出尝试解，然后验证是否满足方程和边界条件。满足即为唯一解，不满足则加以修改。

　　边界条件主要分两类，求解方程会遇到。第一类边界条件，也称狄利克雷（Dirichlet, 1805 – 1859）边界条件，指定微分方程的解在边界处的值。第二类边界条件，也称诺伊曼（Neumann, 1832 – 1925）边界条件，指定边界解的导数。第三类边界条件是一、二类的线性组合。全部是第一类边界，或存在部分第二类边界的情况有唯一解。边界全部是第二类的则没有唯一解。

复变函数

　　谁也没有料到，复变函数能与拉普拉斯算子攀上关系。前者是复数，后者是实数。复解析函数（analytic function）的实部和虚部都满足拉普拉斯方程。换言之，若 z = x + yi，复函数 f(z) = u(x, y) + i v(x, y) ，则 u(x, y) 和 v(x, y) 满足 \nabla ^2 u = \nabla ^2 v = 0 。

　　 f(z) 是解析函数的充要条件是 u(x,y)，v(x,y) 可微，且满足柯西-黎曼方程 \frac {\partial u}{\partial x} = \frac {\partial v}{\partial y},\ \ \frac {\partial u}{\partial y} = -\frac {\partial v}{\partial x} \\

柯西-黎曼方程 \frac {\partial u}{\partial x} = \frac {\partial v}{\partial y},\ \ \frac {\partial u}{\partial y} = -\frac {\partial v}{\partial x} \\

于是， \frac {\partial ^2 u}{\partial x ^2} = \frac {\partial }{\partial x} \big(\frac {\partial u}{\partial x} \big) = \frac {\partial }{\partial x} \big(\frac {\partial v}{\partial y} \big) = \frac {\partial ^2 v}{\partial x \partial y} = \frac {\partial }{\partial y} \big(\frac {\partial v}{\partial x} \big) = \frac {\partial }{\partial y} \big(- \frac {\partial u}{\partial y} \big) = – \frac {\partial ^2 u}{\partial y ^2} ，

 \frac {\partial ^2 u}{\partial x ^2} = \frac {\partial }{\partial x} \big(\frac {\partial u}{\partial x} \big) = \frac {\partial }{\partial x} \big(\frac {\partial v}{\partial y} \big) = \frac {\partial ^2 v}{\partial x \partial y} = \frac {\partial }{\partial y} \big(\frac {\partial v}{\partial x} \big) = \frac {\partial }{\partial y} \big(- \frac {\partial u}{\partial y} \big) = - \frac {\partial ^2 u}{\partial y ^2} ，

移到一边去，就是 \frac {\partial ^2 u}{\partial x ^2} + \frac {\partial ^2 u}{\partial y ^2} = 0 。

 \frac {\partial ^2 u}{\partial x ^2} + \frac {\partial ^2 u}{\partial y ^2} = 0 

留意到中间的 \frac {\partial ^2 v}{\partial x \partial y} = \frac {\partial ^2 v}{\partial y \partial x} ，利用了二阶导数的对称性（Symmetry of second derivatives）：只要函数有连续二阶偏导数，则该函数在那一点的偏导数顺序可交换。同理亦可推，v(x, y)也满足 \frac {\partial ^2 v}{\partial x ^2} + \frac {\partial ^2 v}{\partial y ^2} = 0 。

　　举个例子。 f(z) = z^3 在整个复平面上是解析函数，将 z = x + yi 代入，接着二项式展开得 f(x + yi) = (x + yi)^3 = (x^3 – 3xy^2) + (3x^2y – y^3)i。可以大胆地写下，函数 f(x, y) = x^3 – 3xy^2 与函数 f(x, y) = 3x^2y – y^3 均满足拉普拉斯方程。这也是得到解的一种途径。

坐标系转换

　　先看看二维的直角坐标系转极坐标系。 \nabla ^2 f = \frac {\partial ^2f}{\partial x^2} + \frac {\partial ^2f}{\partial y^2} ，利用链式法则（ chain rule ）有 \frac {\partial f}{\partial x} = \frac {\partial f}{\partial r} \frac {\partial r}{\partial x} + \frac {\partial f}{\partial \theta} \frac {\partial \theta}{\partial x},\ \ \frac {\partial f}{\partial y} = \frac {\partial f}{\partial r} \frac {\partial r}{\partial y} + \frac {\partial f}{\partial \theta} \frac {\partial \theta}{\partial y} ，

\frac {\partial f}{\partial x} = \frac {\partial f}{\partial r} \frac {\partial r}{\partial x} + \frac {\partial f}{\partial \theta} \frac {\partial \theta}{\partial x},\ \ \frac {\partial f}{\partial y} = \frac {\partial f}{\partial r} \frac {\partial r}{\partial y} + \frac {\partial f}{\partial \theta} \frac {\partial \theta}{\partial y} ，

先求一阶导，再求二阶导，达到把变量 x, y 替换成 r, θ 的目的。一阶导数到二阶导数，涉及到 \frac {\partial f}{\partial r} 和 \frac {\partial f}{\partial \theta} 对x的偏导数，仍然用链式法则，推导如下：

\color{blue}{\frac {\partial }{\partial x}\frac {\partial f}{\partial r}} = \frac {\partial }{\partial r}\frac {\partial f}{\partial r} \cdot \frac {\partial r}{\partial x} + \frac {\partial }{\partial \theta}\frac {\partial f}{\partial r} \cdot \frac {\partial \theta}{\partial x} = \frac {\partial ^2f}{\partial r^2} \cdot \frac {\partial r}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \cdot \frac {\partial \theta}{\partial x}

\color{blue}{\frac {\partial }{\partial x}\frac {\partial f}{\partial r}} = \frac {\partial }{\partial r}\frac {\partial f}{\partial r} \cdot \frac {\partial r}{\partial x} + \frac {\partial }{\partial \theta}\frac {\partial f}{\partial r} \cdot \frac {\partial \theta}{\partial x} = \frac {\partial ^2f}{\partial r^2} \cdot \frac {\partial r}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \cdot \frac {\partial \theta}{\partial x}

\color{blue}{\frac {\partial }{\partial x}\frac {\partial f}{\partial \theta}} = \frac {\partial }{\partial r}\frac {\partial f}{\partial \theta} \cdot \frac {\partial r}{\partial x} + \frac {\partial }{\partial \theta}\frac {\partial f}{\partial \theta} \cdot \frac {\partial \theta}{\partial x} = \frac {\partial ^2f}{\partial \theta^2} \cdot \frac {\partial \theta}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \cdot \frac {\partial r}{\partial x}

\color{blue}{\frac {\partial }{\partial x}\frac {\partial f}{\partial \theta}} = \frac {\partial }{\partial r}\frac {\partial f}{\partial \theta} \cdot \frac {\partial r}{\partial x} + \frac {\partial }{\partial \theta}\frac {\partial f}{\partial \theta} \cdot \frac {\partial \theta}{\partial x} = \frac {\partial ^2f}{\partial \theta^2} \cdot \frac {\partial \theta}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \cdot \frac {\partial r}{\partial x}

\begin{align} \frac {\partial ^2 f}{\partial x^2} &= \frac {\partial }{\partial x} \big(\frac {\partial f}{\partial r} \cdot \frac {\partial r}{\partial x} \big)+ \frac {\partial }{\partial x} \big( \frac {\partial f}{\partial \theta} \cdot \frac {\partial \theta}{\partial x} \big) \\ &= \color{blue}{\frac {\partial }{\partial x} \frac {\partial f}{\partial r}} \cdot \frac {\partial r}{\partial x} + \frac {\partial f}{\partial r} \cdot \frac {\partial ^2 r}{\partial x^2} + \color{blue}{\frac {\partial }{\partial x} \frac {\partial f}{\partial \theta}} \cdot \frac {\partial \theta}{\partial x} + \frac {\partial f}{\partial \theta} \cdot \frac {\partial ^2 \theta}{\partial x^2} \\ &= (\frac {\partial ^2f}{\partial r^2} \frac {\partial r}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \frac {\partial \theta}{\partial x}) \frac {\partial r}{\partial x} + \frac {\partial f}{\partial r} \frac {\partial ^2 r}{\partial x^2} + (\frac {\partial ^2f}{\partial \theta^2} \frac {\partial \theta}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \frac {\partial r}{\partial x}) \frac {\partial \theta}{\partial x} + \frac {\partial f}{\partial \theta} \frac {\partial ^2 \theta}{\partial x^2} \\ &= \color{green}{\frac {\partial ^2f}{\partial r^2}} (\frac {\partial r}{\partial x})^2 + \color{green}{2\frac {\partial ^2 f}{\partial r \partial \theta}} \frac {\partial \theta}{\partial x} \frac {\partial r}{\partial x} + \color{green}{\frac {\partial ^2 f}{\partial \theta ^2}} (\frac {\partial \theta}{\partial x})^2 + \color{green}{\frac {\partial f}{\partial r}} \frac {\partial ^2 r}{\partial x^2} + \color{green}{\frac {\partial f}{\partial \theta}} \frac {\partial ^2 \theta}{\partial x^2} \end{align}

\begin{align} \frac {\partial ^2 f}{\partial x^2} &= \frac {\partial }{\partial x} \big(\frac {\partial f}{\partial r} \cdot \frac {\partial r}{\partial x} \big)+ \frac {\partial }{\partial x} \big( \frac {\partial f}{\partial \theta} \cdot \frac {\partial \theta}{\partial x} \big) \\ &= \color{blue}{\frac {\partial }{\partial x} \frac {\partial f}{\partial r}} \cdot \frac {\partial r}{\partial x} + \frac {\partial f}{\partial r} \cdot \frac {\partial ^2 r}{\partial x^2} + \color{blue}{\frac {\partial }{\partial x} \frac {\partial f}{\partial \theta}} \cdot \frac {\partial \theta}{\partial x} + \frac {\partial f}{\partial \theta} \cdot \frac {\partial ^2 \theta}{\partial x^2} \\ &= (\frac {\partial ^2f}{\partial r^2} \frac {\partial r}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \frac {\partial \theta}{\partial x}) \frac {\partial r}{\partial x} + \frac {\partial f}{\partial r} \frac {\partial ^2 r}{\partial x^2} + (\frac {\partial ^2f}{\partial \theta^2} \frac {\partial \theta}{\partial x} + \frac {\partial ^2 f}{\partial r \partial \theta} \frac {\partial r}{\partial x}) \frac {\partial \theta}{\partial x} + \frac {\partial f}{\partial \theta} \frac {\partial ^2 \theta}{\partial x^2} \\ &= \color{green}{\frac {\partial ^2f}{\partial r^2}} (\frac {\partial r}{\partial x})^2 + \color{green}{2\frac {\partial ^2 f}{\partial r \partial \theta}} \frac {\partial \theta}{\partial x} \frac {\partial r}{\partial x} + \color{green}{\frac {\partial ^2 f}{\partial \theta ^2}} (\frac {\partial \theta}{\partial x})^2 + \color{green}{\frac {\partial f}{\partial r}} \frac {\partial ^2 r}{\partial x^2} + \color{green}{\frac {\partial f}{\partial \theta}} \frac {\partial ^2 \theta}{\partial x^2} \end{align}

　　同理，上式中的x全部替换成y，得到 \frac {\partial ^2 f}{\partial y^2} 的表达式。两者相加得到 \frac {\partial ^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2} ，需要合并对应的项。上述推导与极坐标无关，仅表示二元函数的二阶偏导数，下面的推导才开始引入极坐标。接下来要计算 r, θ 分别对 x, y 的一阶、二阶偏导数。

\begin{equation} \begin{cases} x = r \cos \theta \\ y = r \sin \theta \\ \end{cases} \end{equation} 中，x, y 分别对 r, θ 求偏导有 \begin{equation} \begin{cases} \frac {\partial x}{\partial r} = \cos \theta,\ \frac {\partial x}{\partial \theta} = -r \sin \theta \\ \frac {\partial y}{\partial r} = \sin \theta,\ \ \frac {\partial y}{\partial \theta} = r \cos \theta \\ \end{cases} \end{equation} 。对比上面的式子，发现谁对谁求导弄颠倒了，所以能上下翻过来变成倒数使用吗？不能！这是偏微分，不是微分。若反函数存在，则微分存在倒数关系 \frac {dy}{dx} \cdot \frac {dx}{dy} = 1 [7]。

　　将r和θ用变量 x, y 表示有r = \sqrt{x^2 + y^2} 。x和y相除，可消去r，有 \frac y x = \tan \theta 。有关系 \begin{equation} \begin{cases} r^2 = x^2 + y^2 \\ \tan \theta = y / x \\ \end{cases} \end{equation} 。r, θ分别对 x, y 求偏导有 \begin{equation} \begin{cases} \frac {\partial r}{\partial x} = \cos \theta,\ \ \ \ \frac {\partial r}{\partial y} = \sin \theta \\ \frac {\partial \theta}{\partial x} = -\frac {\sin \theta}{r},\ \ \frac {\partial \theta}{\partial y} = \frac {\cos \theta}{r} \\ \end{cases} \end{equation}

我们看到 r^2 = x^2 + y^2 两边对 x 求导，有 2r \frac {\partial r}{\partial x} = 2x ，可以马上得到 \frac {\partial r}{\partial x} = \frac x r 。该式x和y位置可轮换，所以也有 \frac {\partial r}{\partial y} = \frac y r 。如果用式子 r = \sqrt{x^2 + y^2}去求导就显得繁琐些，虽然结果一致。 \frac {\partial r}{\partial x} = \big ( (x^2 + y^2)^{\frac 1 2} \big) ‘ = \frac 1 2 (x^2 + y^2)^{-\frac 1 2} \cdot \frac {d (x^2 + y^2)}{d x} = \frac x {\sqrt{x^2 + y^2}} = \frac x r 。将 x = r \cos \theta,\ y = r \sin \theta 分别代入后有 \frac {\partial r}{\partial x} = \cos \theta,\ \frac {\partial r}{\partial y} = \sin \theta 。至此也能说明， \frac {\partial x}{\partial r} 与 \frac {\partial r}{\partial x} 不是倒数关系。 \frac {\partial x}{\partial r} = \frac {\partial r}{\partial x} = \cos \theta ， \frac {\partial y}{\partial r} = \frac {\partial r}{\partial y} = \sin \theta ，竟然相等上了。对 \tan x 求导得 \sec^2 x ，式子 \tan \theta = y / x 两边对 x 求导得 \sec^2 \theta\ \frac {d \theta}{dx} = y \cdot (- \frac 1 {x^2}) ，对y求导得 \sec^2 \theta \frac {d \theta}{dy} = \frac 1 x ，接着 \frac {d \theta}{dx} = – \frac {y \cos^2 \theta } {x^2} = – \frac {r \sin \theta \cdot \cos^2 \theta } {(r \cos \theta)^2} = -\frac {\sin \theta}{r} ，以及

\frac {d \theta}{dy} = \frac {\cos^2 \theta}{x} = \frac {\cos^2 \theta}{r \cos \theta} = \frac {\cos \theta}{r} 。

　　用一阶偏微分式子 \frac {\partial r}{\partial x} = \frac x r 计算二阶偏微分。

\frac {\partial ^2r}{\partial x^2} = \frac {\partial}{\partial x} (\frac x r) = \frac {x^{‘} r – x r^{‘}}{r^2} = \frac {r – x \frac {dr}{dx}}{r^2} = \frac {r – x \frac {x}{r}} {r^2} = \frac {r^2 – x^2}{r^3} = \frac {y^2}{r^3}

因为 r^2 = x^2 + y^2 ，x与y位置可轮换，是轮换式，于是 \frac {\partial ^2r}{\partial y^2} = \frac {x^2}{r^3} 。式子 \tan \theta = y / x 中的x与y位置不能轮换，所以需要分别求 \frac {\partial ^2 \theta}{\partial x^2} 和 \frac {\partial ^2 \theta}{\partial y^2} 。 \frac {\partial ^2 \theta}{\partial x^2} = \frac {\partial }{\partial x} (-\frac {\sin \theta}{r}) = \frac {\partial }{\partial x} (-\frac {r \sin \theta}{r^2}) = \frac {\partial }{\partial x} (-\frac {y}{r^2}) = -y \frac {\partial }{\partial x} (r^{-2}) = -y (-2) r^{-3} \frac {dr}{dx} = \frac {2y}{r^3} \frac x r = \frac {2xy}{r^4}

\frac {\partial ^2 \theta}{\partial y^2} = \frac {\partial }{\partial y} (\frac {\cos \theta}{r}) = \frac {\partial }{\partial y} (\frac {r \cos \theta}{r^2}) = \frac {\partial }{\partial y} (\frac {x}{r^2}) = x \frac {\partial }{\partial y} (r^{-2}) = x (-2) r^{-3} \frac {dr}{dy} = \frac {-2x}{r^3} \frac y r = -\frac {2xy}{r^4}

回到开始与极坐标无关的式子，相加后为

\nabla ^2 f = \color{green}{\frac {\partial ^2f}{\partial r^2}} \big[(\frac {\partial r}{\partial x})^2 + (\frac {\partial r}{\partial y})^2 \big] + \color{green}{2\frac {\partial ^2 f}{\partial r \partial \theta}} \big[ \frac {\partial \theta}{\partial x} \frac {\partial r}{\partial x} + \frac {\partial \theta}{\partial y} \frac {\partial r}{\partial y} \big] + \color{green}{\frac {\partial ^2 f}{\partial \theta ^2}} \big[(\frac {\partial \theta}{\partial x})^2 + (\frac {\partial \theta}{\partial y})^2 \big] + \color{green}{\frac {\partial f}{\partial r}} \big[ \frac {\partial ^2 r}{\partial x^2} + \frac {\partial ^2 r}{\partial y^2} \big] + \color{green}{\frac {\partial f}{\partial \theta}} \big[ \frac {\partial ^2 \theta}{\partial x^2} + \frac {\partial ^2 \theta}{\partial y^2}\big]

第一项的系数 (\frac {\partial r}{\partial x})^2 + (\frac {\partial r}{\partial y})^2 = \cos^2 \theta + \sin ^2 \theta = 1

第二项的系数 \frac {\partial \theta}{\partial x} \frac {\partial r}{\partial x} + \frac {\partial \theta}{\partial y} \frac {\partial r}{\partial y} = -\frac {\sin \theta}{r} \cdot \cos \theta + \frac {\cos \theta}{r} \cdot \sin \theta = 0

第三项的系数 (\frac {\partial \theta}{\partial x})^2 + (\frac {\partial \theta}{\partial y})^2 = (-\frac {\sin \theta}{r})^2 + (\frac {\cos \theta}{r} )^2 = \frac 1 {r^2}

第四项的系数 \frac {\partial ^2 r}{\partial x^2} + \frac {\partial ^2 r}{\partial y^2} = \frac {y^2}{r^3} + \frac {x^2}{r^3} = \frac {r^2}{r^3} = \frac 1 r

第五项的系数 \frac {\partial ^2 \theta}{\partial x^2} + \frac {\partial ^2 \theta}{\partial y^2} = \frac {2xy}{r^4} – \frac {2xy}{r^4} = 0

代入上面的式子中，得到拉普拉斯算子在极坐标下的表示 \nabla ^2 f = \frac {\partial ^2f}{\partial r^2} + \frac 1 r \frac {\partial f}{\partial r}+\frac 1 {r^2} \frac {\partial ^2 f}{\partial \theta ^2} 。可以看到，推导过程很繁琐，因为链式法则会引入越来越多的项，中途会抵消一些项，结果迈向简单。

三维解

　　接着来到三维世界 \nabla ^2 f = \frac {\partial ^2 f}{\partial x^2} + \frac {\partial ^2 f}{\partial y^2} + \frac {\partial ^2 f}{\partial z^2} = 0 。可以参考上面二维解加法和乘法的思路求解，这里不赘述了。

　　下面给出三维空间情况下拉普拉斯算子的表示，分别为空间直角坐标系、柱面坐标系、球面坐标系。从平面极坐标系 (r, θ) 到空间柱面坐标系(r, θ, z)，从二维升到三维，添加的z轴与 r 和 θ 相互独立，所以，末尾直接追加 \frac {\partial ^2 f}{\partial z^2} 即可得到柱面坐标系下的 \nabla ^2 f 。球面坐标系可以照着上面的步骤自行推导。

\begin{align} f(x, y, z) \rightarrow \nabla ^2 f &= \frac {\partial ^2f}{\partial x^2} + \frac {\partial ^2f}{\partial y^2} + \frac {\partial ^2f}{\partial z^2} \\ f(r, \theta, z) \rightarrow \nabla ^2 f &= \frac 1 r \frac {\partial}{\partial r} \big( r \frac {\partial f}{\partial r}\big) + \frac 1 {r^2} \frac {\partial ^2 f}{\partial \theta ^2} + \frac {\partial ^2 f}{\partial z^2} \\ f(r, \theta, \phi) \rightarrow \nabla ^2 f &= \frac 1 {r^2} \frac {\partial}{\partial r} \big( r^2 \frac {\partial f}{\partial r}\big) + \frac 1 {r^2 \sin \theta} \frac {\partial}{\partial \theta} \big(\sin \theta \frac {\partial f}{\partial \theta} \big) + \frac 1 {r^2 \sin^2 \theta} \frac {\partial ^2 f}{\partial \phi^2} \end{align}

　　来看看仅与距离 r 有关的拉普拉斯方程的解，极坐标系 f(r, θ) 或柱面坐标系f(r, θ, z)下，假设 f 只与距离 r 有关，与角θ、高度z无关，有 \frac 1 r \frac {\partial}{\partial r} \big( r \frac {\partial f}{\partial r}\big) = 0 ，继续推导 \frac {\partial}{\partial r} \big( r \frac {\partial f}{\partial r}\big) = 0 ⇒ r \frac {\partial f}{\partial r} = c ⇒ \frac {\partial f}{\partial r} = \frac {c} {r} ⇒ f(r, θ, z) = c \ln r 。其中 c 为任意常数。于是，三维坐标系下的一种解为 f(r, θ, z) = \ln r 或 f(x, y) = \ln ({x^2 + y^2}),\ f(x, y, z) = \ln ({x^2 + y^2})。注意到开方操作在 ln 下，可以提取出常系数而扔掉。

　　解球面坐标系下的拉普拉斯方程，会得到球面上的谐和函数，即球谐函数（Spherical Harmonics）。假设球面坐标系下的函数 f(r, θ, ϕ) 只与距离 r 有关，与方位角θ、ϕ无关，即 f 关于θ、ϕ的偏微分相当于对常数求导， \frac {\partial f}{\partial \theta} = \frac {\partial f}{\partial \phi} = 0 ，可抹去。得到 \nabla ^2 f = \frac 1 {r^2} \frac {\partial}{\partial r} \big( r^2 \frac {\partial f}{\partial r}\big) = 0 ，继续推导 \frac {\partial}{\partial r} \big( r^2 \frac {\partial f}{\partial r}\big) = 0 ⇒ r^2 \frac {\partial f}{\partial r} = c ⇒ \frac {\partial f}{\partial r} = \frac {c} {r^2} ⇒ f(r, θ, ϕ) = -\frac c r 。其中 c 为任意常数，所以负号和常数可以塞给它吸收，得到 f(r, θ, ϕ) = \frac c r 。于是，三维坐标系下的一种解为 f(r, θ, ϕ) = \frac 1 r 或 f(x, y, z) = \frac 1 {\sqrt{x^2 + y^2 + z^2}} 。

数字图像处理

　　如果只是解微分方程，略显枯燥。能给出具体场景应用，就有意思了。SIGGRAPH 2003 出现一篇论文

图像泊松融合

《Poisson Image Editing》(Christopher J. Tralie, Ph.D.)，可以无缝衔接两张图。OpenCV 3 实现该功能后取名为 Seamless Cloning。这里介绍了关于泊松方程在图像和形状相关的应用[8]，对图像的编辑，给出了5篇 SIGGRAPH 论文，可结合理论深入学习。

• Poisson Image Editing
• Seamless Image Stitching in the Gradient Domain
• Interactive Digital Photomontage
• Drag-and-Drop Pasting
• Efficient Gradient-Domain Compositing Using Quadtrees

　　无缝融合图像是以源图像块内的梯度场为向导，将融合边界上目标场景和源图像的差异平滑地扩散到融合图像块中，该操作使得，融合后的图像块能够无缝地融合到目标场景中，并且其色调和光照可以与目标场景保持一致。

以v为梯度场，f*的接壤处为边界Ω，可参考梯度场g，求解未知函数f

seamlessClone(src, dst, mask, center, output, NORMAL_CLONE);

参考

1. ^以拉普拉斯命名的事物 https://en.wikipedia.org/wiki/List_of_things_named_after_Pierre-Simon_Laplace
2. ^拉普拉斯方程 https://en.wikipedia.org/wiki/Laplace%27s_equation
3. ^是公式都会追求短而美 https://www.zhihu.com/question/26992291/answer/1448275421
4. ^可分离变量的偏微分方程 https://en.wikipedia.org/wiki/Separable_partial_differential_equation
5. ^解二阶常系数齐次线性微分方程 https://en.wikipedia.org/wiki/Linear_differential_equation#Second-order_case
6. ^唯一性定理 https://en.wikipedia.org/wiki/Uniqueness_theorem_for_Poisson%27s_equation
7. ^反函数及其微分 https://en.wikipedia.org/wiki/Inverse_functions_and_differentiation
8. ^The Poisson Equation in Image & Shape Processing https://www.cs.jhu.edu/~misha/Fall07/

编辑于 2023-04-22 19:33・IP 属地中国香港

《Poisson Image Editing》论文理解与复现

2023年4月9日 本报告的主要内容是阅读《Poisson Image Editing》论文之后对原理进行理解并利用python复现论文中的每个功能。 2. 引言 图像融合是图像处理的一个基本问题,目的是将源图像中一个物体…

betheme.net/yidongkaifa/42…html